
|
|
|
|
#1 (ссылка) |
|
Crow indian
Регистрация: 21.02.2009
Возраст: 40
Сообщений: 30,045
Поблагодарил: 398 раз(а)
Поблагодарили 5988 раз(а)
Фотоальбомы:
2576 фото
Записей в дневнике: 698
Репутация: 126089
|
Тема: [12-2023] Классификация состояний стрелочного переводаКлассификация состояний стрелочного перевода КАНАРСКИЙ Вадим Андреевич, Дальневосточный государственный университет путей сообщения, кафедра «Автоматика, телемеханика и связь», преподаватель, г. Хабаровск, Россия Ключевые слова: стрелочный перевод, неисправность, временные ряды, мощность, преобразование Фурье, машинное обучение, классификация Аннотация. При мониторинге стрелочного перевода в основном используются методы электрической диагностики. Однако недостаток контролируемых при этом параметров приводит к неспособности системы мониторинга в полной мере описать неисправный узел. Вместе с этим существуют косвенные методы оценки состояния устройства на основе спектрального анализа сигналов, вырабатываемых электродвигателем во время перевода. Совместив такой подход с технологиями искусственного интеллекта можно выделить неявную информацию и представить ее в виде интерпретируемого результата. Были исследованы характеристики активной мощности, полученные при диагностике силовых параметров устройств, функционирующих в составе АПК-ДК. В результате дискретного преобразования Фурье обоснован выбор подходящих гармоник, проведен сравнительный анализ алгоритмов контролируемого машинного обучения в решении задачи классификации состояния стрелочного перевода. Стрелочный перевод представляет собой один из самых уязвимых и критически важных объектов железнодорожной инфраструктуры. Эти устройства испытывают огромную динамическую нагрузку, и согласно информации Управления автоматики и телемеханики ЦДИ на них приходится примерно 8 % всех отказов технических средств. При этом проводимые планово-предупредительные мероприятия по технологическим картам не дают гарантии предотвращения повреждений переводов. Система технической диагностики и мониторинга (СТДМ) в электрической централизации заменяет ручные измерения тока, напряжения и сопротивления устройств. На сети железных дорог более 68 % станций оборудованы аппаратно-программными комплексами диспетчерского контроля (АПК-ДК). Используемый в составе АПК-ДК автомат диагностики параметров стрелочного электропривода АДСП позволяет зафиксировать напряжения и токи трех фаз, мощность и тяговое усилие [1]. Однако стрелочный перевод является более сложным механизмом и такого контроля для определения его предотказного состояния недостаточно. За последние годы применялись различные подходы к усовершенствованию СТДМ, один из которых заключался в реализации контроля параметров неэлектрической при роды. Применение методов, основанных на анализе вибрации узлов электропривода или напряженности магнитного поля электродвигателя, в существующих системах технической диагностики и мониторинга требуют оснащения каждой стрелки дополнительными датчиками, что влечет за собой существенные финансовые затраты [2]. Поводом для данного исследования стала работа [3], в которой были проведены натурные эксперименты на стрелочном переводе, позволившие установить соответствие формы графика активной мощности одной из восьми категорий неисправности. Установлено, что исправный перевод описывается характеристикой, представленной на рис. 1.  Путем имитации поломок и исследований архивов мониторинга различных неисправностей были составлены графики определенной формы, амплитуды и длительности [3]. Моменты проявления неисправностей на графиках мощности продемонстрированы на рис. 2, где состояние «1» - грязные или несмазанные стрелочные башмаки; состояние «2» - наличие переходного сопротивления в фазах электродвигателя; состояние «3» - непараллельное прилегание остряка к рамному рельсу; состояния «4,5» - разрегулировка фрикционного сцепления в сторону уменьшенного/ увеличенного усилия работы на фрикцию; состояние «6» - пружинность стрелочных остряков. На рис. 1, 2 точки кривых зафиксированы автоматами диагностики силовых параметров (АДСП) с шагом дискретизации 0,02 с. Данные последовательности являются функциями времени, и для них можно определить гармонический состав, чтобы понять внутреннюю структуру каждой категории сигнала. Подобный математический аппарат уже был использован в отношении переменного и постоянного токов рабочей цепи [4]. Предложенный метод компьютерной диагностики позволил по изменению амплитудных и частотных составляющих делать вывод о состоянии стрелочного перевода. Для двигателей постоянного тока (МСП) при нормальном переводе стрелки установлены три гармонические составляющие [5]. При отклонении режима от нормального в спектре появляются еще три компонента, возникающие из-за ухудшения условий коммутации, загрязнения коллектора графитовой пылью или при обрывах (или коротком замыкании) секций якоря. Таким образом, было обосновано применение аналитического метода определения характера неисправности для двигателей МСП. Основной идеей в исследованиях [4, 5] было определение состояния стрелочного перевода на основе наличия определенных спектральных компонентов при возникновении каких-либо неисправностей. Особенность этого подхода заключается в том, что пространство спектров по своей природе абстрактно, но при этом обладает некоторой регулярностью, т.е. для каждого типа неисправности существует определенный набор гармонических компонентов. Неявная информация, заключенная в этом пространстве, может быть использована в качестве входных данных для алгоритмов контролируемого машинного обучения (supervisory machine learning, ML). Модели ML, обучившись на размеченных входных данных, способны решать задачу классификации [6], предоставляя оператору более понятные и интерпретируемые результаты. Общая структурная схема обработки исходных данных представлена на рис. 3. Распространенным математическим инструментом, позволяющим получить амплитудно-частотные характеристики, является дискретное преобразование Фурье (ДПФ): 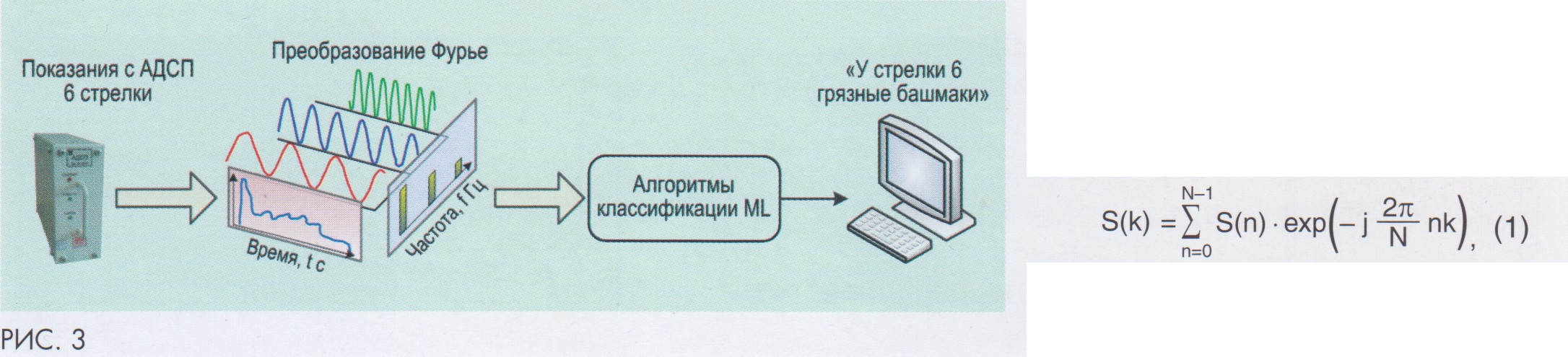 где S(k) - амплитудное значение спектрального отсчета; к - номер гармоники; N - количество отсчетов исходного сигнала; п - индекс отсчета исходной временной зависимости. Частоты, соответствующие спектральным отсчетам, определяются по формуле: 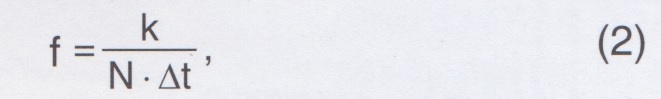 где At - период дискретизации АДСП (0,02 с). Согласно выражению (1) каждому дискретному отсчету возвращается свой спектральный отсчет, и для каждой кривой разной длительности будет свой набор гармонических составляющих, что является проблемой для обучения моделей ML, для которых требуются векторы постоянной длины. Проанализировать вклад некоторых гармоник можно по табл. 1, где представлен спектральный состав графиков мощности каждого класса состояний стрелочного перевода в процентном соотношении. 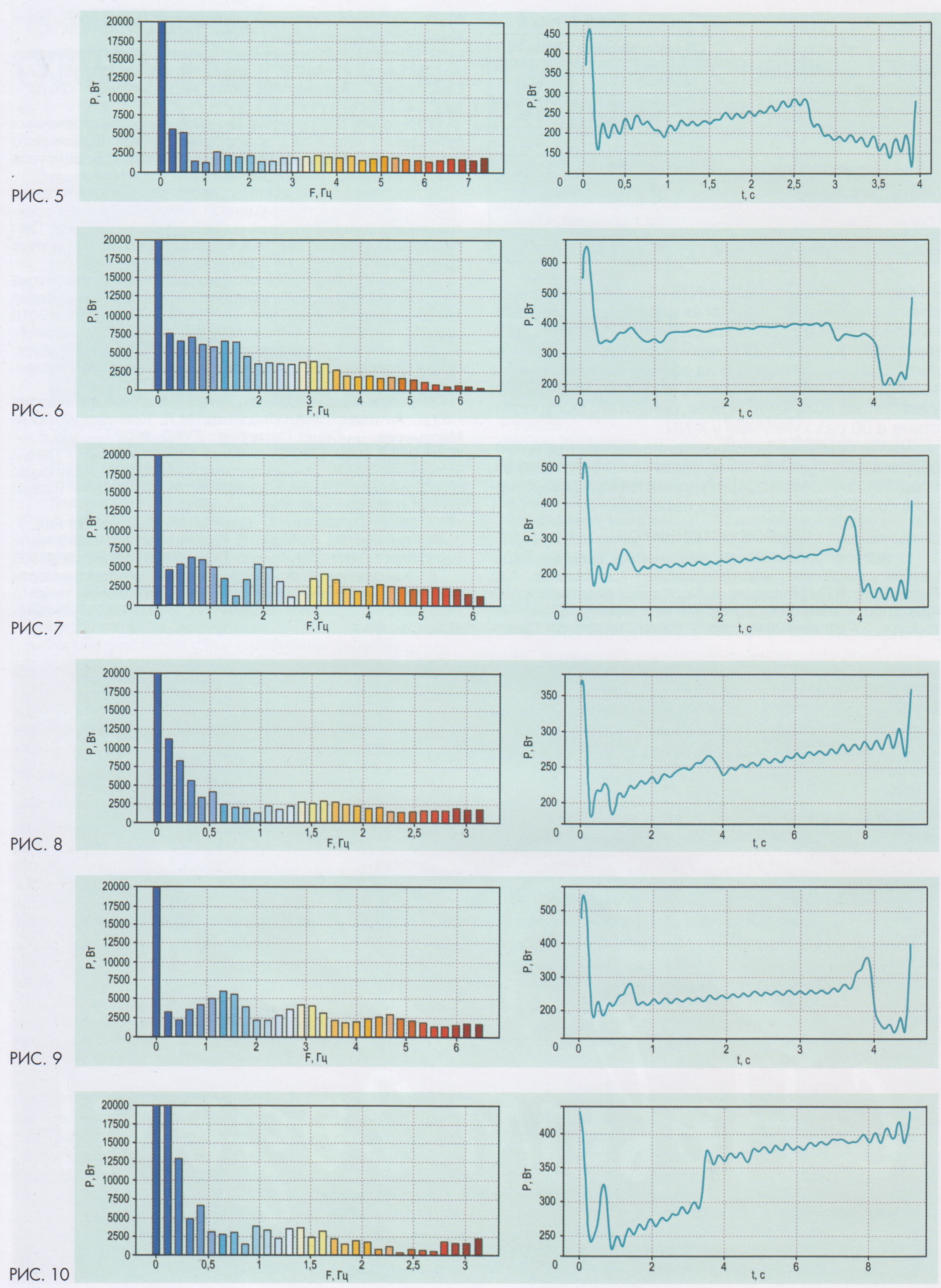 Из данных табл. 1 видно, что гармоники старше 40-й (выделены красным) имеют наименьшую амплитуду (меньше 0,5 % от общего вклада всех гармонических амплитуд) и слабо различаются между собой в семи разных состояниях, а значит не обладают полезной информацией для классификаторов. Основная энергия сигналов сосредоточена на низких частотах, и именно они позволяют сохранить большую часть информации временного ряда. Таким образом, вместо графиков, построенных из =200-400 точек (см. рис. 1 и 2) и имеющих разную длительность и форму, для классификации будут использоваться только их первые 30 содержательных гармоник. Данное решение позволяет снизить размерность входных данных до 30, а также установить ее постоянной (чего нельзя достичь при непосредственном использовании графиков, длительность которых зависит от времени перевода стрелки и является непостоянной). Ограничение сигналов мощности 30-тью гармониками также позволяет избавиться от шума, вызванного высокочастотными низкоамплитудными спектральными составляющими, препятствующими нормальной работе классификаторов. Для доказательства достоверности принятого решения с помощью обратного преобразования Фурье восстановлены кривые мощности на извлеченных 30-ти гармониках у состояний «0-6» стрелочного перевода (рис. 4-10). При сравнении восстановленных сигналов (см. рис. 4—10) с представленными оригиналами (см. рис. 1, 2) отмечается их схожесть, т.е. представлять образ того или иного класса вполне способны первые 30 гармонических компонент. Как было отмечено в [5], общий характер зависимости амплитуд гармоник от частоты (гистограмм на рис. 4-10) - экспоненциальный. Частотный диапазон для всех исследуемых состояний стрелочного переводного устройства находится в пределах 0-25 Гц. Ограничение в тридцать гармоник показывает, что основная информация у состояний «4» и «5» заключена до 3 Гц, у остальных - до 7 Гц. 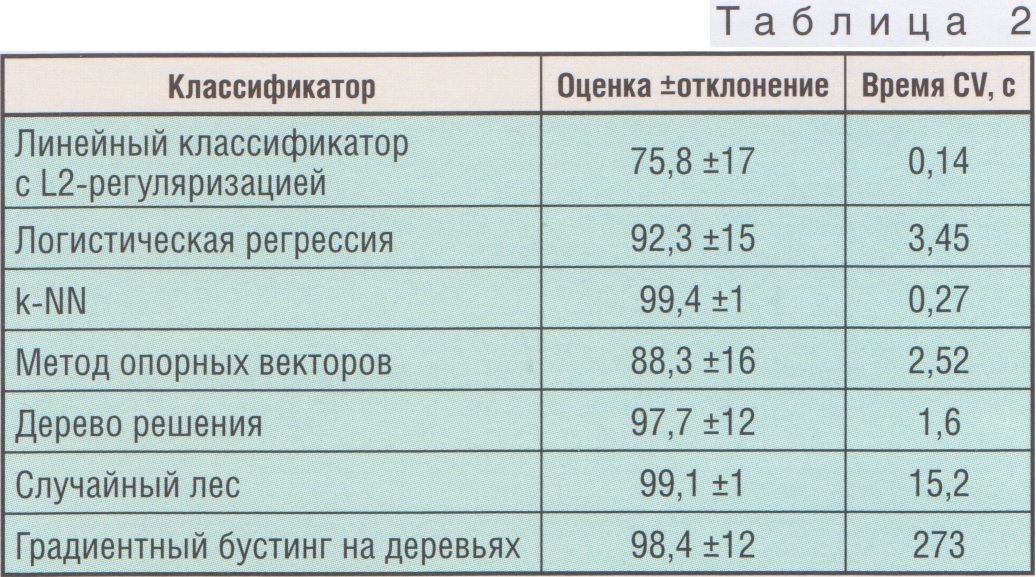 На языке программирования Python с помощью библиотеки Scikit-learn были импортированы и протестированы семь классификаторов [7] с параметрами по умолчанию. Показателем качества в данном случае выступает интуитивно понятная метрика «точность» (accuracy) [8], характеризуемая отношением количества верно определенных состояний СП (correct) к количеству всех состояний в обучающей выборке (total). Способ оценки заключается в разделении набора данных на 20 равных частей. Затем классификаторы обучаются случайным образом на 19 частях, а на 20-й части выполняется тестирование. Результаты классификации на матрице гармонических амплитуд представлены в табл. 2. Этот процесс, известный как перекрестная валидация CV (cross-validation), обеспечивает более надежную усредненную оценку со среднеквадратичным отклонением. Вычислительный эксперимент показал, что согласно информации, представленной в табл. 2, алгоритм «к-ближайших соседей» k-NN (k-Nearest Neighbors) на спектральных компонентах активной мощности двигателя позволяет автоматически классифицировать неисправность стрелки с вероятностью 99,4 ±1 %, что является лучшей оценкой из всех, представленных в табл. 2. Также высокая степень точности наблюдается у алгоритма «Случайный лес», однако его быстродействие в 60 раз хуже, чем у k-NN. Таким образом, использование дискретного преобразования Фурье в совокупности с алгоритмами ML представляет собой эффективный метод компьютерного состояния стрелочного перевода. СПИСОК ИСТОЧНИКОВ 1. Иванов, А.А. Автомат диагностики силовых параметров стрелочного электропривода / А.А. Иванов, А.К. Легоньков, В.П. Молодцов // Проблемы безопасности и надежности микропроцессорных комплексов, Санкт-Петербург, 27-28 мая 2015 года. - Санкт-Петербург: Петер бургский государственный университет путей сообщения Императора Александра I, 2015. - С. 110-117. 2. Котов, В.К. Диагностика стрелочных электроприводов по параметрам тока / В. К. Котов, А. А. Павловский, Е. А. Павловский // Автоматика, связь, информатика. - 2015. -№ 7.-С. 12-17. 3. Белоусов С.В. Проявление неисправностей стрелочных переводных устройств с электродвигателями переменного тока на графике мощности перевода [Текст] / С.В. Белоусов // Автоматика на транспорте. - 2018. - Т.4 - № 4. 4. Дистанционное диагностирование состояния стрелочных переводов по временной характеристике и спектральному составу токовой кривой / С.Ю. Буряк, В.И. Гав-рилюк, О.А. Гололобова, М.А. Ковригин // Наука и прогресс транспорта. - 2015. - № 2(56). - С. 39-57. 5. Сердюк, Т.Н. Диагностика двигателей постоянного тока стрелочных приводов/Т.Н. Сердюк//Завалишинские чтения 16: сборник докладов, Санкт-Петербург, 11-15 апреля 2016 года / Санкт-Петербургский государственный университет аэрокосмического приборостроения. - Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2016. - С. 217-224. 6. Основы искусственного интеллекта: учебное пособие / Ю.А. Антохина, А.А. Оводенко, М.Л. Кричевский, Ю.А. Мартынова. — Санкт-Петербург: ГУАП, 2022. — 169 с. — ISBN 978-5-8088-1720-3. — Текст : электронный // Лань : электронно-библиотечная система. — URL: https://e.lanbook. com/book/263933 (дата обращения: 05.08.2023). — Режим доступа: для авториз. пользователей. 7. Grisel, О., Mueller, A., Gramfort, A., Louppe, G., Fan, Т. J., Prettenhofer, Р.,. Woolam, С. (2023). scikit-learn/scikit-learn: Scikit-learn 1.3.0 (1.3.0). Zenodo. DOI: 10.5281/zenodo.8098905 8. Канарский В.А. Исследование эффективности машинного обучения в мониторинге сигнальной точки // Надежность. 2023. № 1. С. 38-44. DOI: 10.21683/1729-2646-2023-23-1-38-44 |
|
|
Цитировать 12 |
|
|
||||
| Тема | Автор | Раздел | Ответов | Последнее сообщение |
| Помогите найти документ, определяющий границы осблуживания ручного стрелочного перевода | Sergey10005 | Поиск документации | 0 | 26.11.2012 16:00 |
| =Курсовая работа= Расчет и проектирование рельсовой колеи и одиночного обыкновенного стрелочного перевода | Admin | Студенту-путeйцу | 0 | 11.07.2012 14:10 |
| Раскладка стрелочного перевода Р 43 | Саня 1111 | Путейцы | 1 | 29.03.2012 12:10 |
| Взрез стрелочного перевода. ДСП-ДНЦ. | chaukova | Курсовое и дипломное проектирование | 3 | 12.11.2010 04:45 |
| Взрез стрелочного перевода. | chaukova | Курсовое и дипломное проектирование | 6 | 09.09.2010 18:34 |
| Ответить в этой теме Перейти в раздел этой темы Translate to English |
| Возможно вас заинтересует информация по следующим меткам (темам): |
| , , , , |
| Здесь присутствуют: 1 (пользователей: 0 , гостей: 1) | |
|
|