13.7. Расчет токосъема для токоприемников

с двумя степенями свободы, с учетом контактных подвесок

с сосредоточенными параметрами

 

Предлагаемый метод расчета разработан в МИИТе А.В. Фрайфельдом (с элементами метода И.И. Власова) и базируется на решении системы двух дифференциальных неоднородных линейных уравнений с коэффициентами, значение которых неодинаково в разных точках пролета.

К основным допущениям метода относятся следующие:

- контактная подвеска является системой с сосредоточенными параметрами;

- нелинейность (от высоты, скорости) характеристики токоприемника, эффекты приведения (к месту в пролете) и инерционные эффекты не принимаются во внимание;

- контактное нажатие определяется без учета отрывов и распределения по пластинам (вставкам);

- сосредоточенные параметры, входящие в расчетную схему подвески (рис. 13.20, а): высотного положения Н_кас(х),  жесткости ж_с(х), массы m_с(х), силы сухого трения W_c(x) и коэффициента вязкого трения r_c (х) меняют свои размеры в разных точках пролета. Эти зависимости определяют экспериментально или расчетом с использованием точных или приближенных (парабола, синусоида и т. д.) уравнений. В программу расчетов на ЭВМ они вводятся таблицей по шагам или уравнениями.

Значения сил сухого трения могут считаться не зависящими от скорости движения элементов, но их знаки меняются каждый раз при изменении направления движения. Силы трения направлены навстречу движению. Это следует учитывать в уравнениях специальными функциями с символами sign, которые, будучи записаны после какой-либо величины, дают ей знак другой величины, записанной после этого символа. Так, для силы трения W учитывается знак скорости движения (зависящей от направления движения), т.е. W sign Н. Силы трения являются нелинейными элементами в системе.

Силы вязкого трения в системе «токоприемник — подвеска» в рассматриваемом методе упрощенно принимают линейными, пропорциональными первой степени скорости движения, и могут быть найдены через коэффициенты вязкого трения (r_с, r_к, r_p) как r Н.

Силы, создаваемые упругими элементами (обладающими жесткостью или эластичностью), принимаются линейными, т. е. прямо пропорциональными их напряжению сжатия (для кареток) или отжатия (для проводов). Тогда с учетом жесткости (ж_с, ж_к, ж_р) можно записать ж_с (Н_с- H_кас); ж_к (Н_п - Н_p - h_ко) и т.д. В последнем выражении h_ко представляет собой расстояние от верхней поверхности полоза до середины верхнего шарнира токоприемника (при освобожденных пружинах). Следует отметить, что нажатие рам (статическая характеристика) принимается постоянным, не зависящим от высоты, что допустимо для средней части рабочего диапазона высоты.

Составление уравнений при наличии расчетной схемы следует начинать с выявления масс, которые могут находиться в независимом вертикальном движении, т.е. с установления числа степеней свободы (подвижностей), определяющих число дифференциальных уравнений, из которых должна состоять система, и число неизвестных, которые должны быть определены.

При составлении уравнений направление снизу вверх принимают положительным для сил Р, скоростей  и  ускорений .

Из расчетной схемы видно, что в рассматриваемой системе имеются две степени свободы: положения масс сети m_с и полоза m_п определяются высотой H_п, положения массы рам — координатой Н_p .

Уравнение движения масс m_с и m_п можно составить (рис. 13.20,б), найдя сумму сил. По второму закону Ньютона масса (массы), на которую действует сила (силы), должна двигаться с ускорением, пропорциональным этой силе. Составим уравнение этого движения, учитывая направление сил (рис. 13.20, г):

 

 

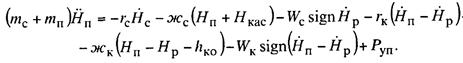
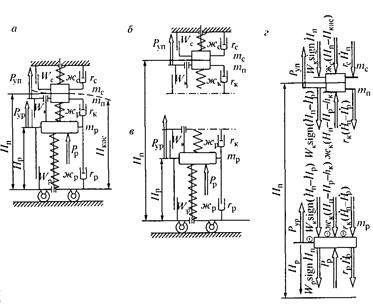
Рис. 13.20. Схемы к составлению уравнений движения для токоприемников с двумя степенями свободы при сосредоточенных параметрах контактной подвески

 

Знак «минус» перед упругой силой кареток объясняется тем, что выражение в скобках отрицательно.

Уравнение движения массы т составим, учитывая направление сил (рис. 13.21, б, в, г):

Знак «плюс» перед силами кареток вместо «минус» в соответствии с направлением сил объясняется отрицательными значениями в скобках, если принять H_п = 0.

Эти уравнения можно решать численным методом на ЭВМ. Для этого надо разделить пролет на интервалы (шаги для ЭВМ). Уравнение составлено по времени, поэтому место в пролете для каждого значения полученных траекторий можно найти, умножая его на скорость поезда.

Уравнения контактного нажатия можно получить двумя способами: заменив реакцией действие проводов подвески на полоз (рис. 13.21, а, б) или действие полоза на подвеску (рис. 13.21, в, г).

 

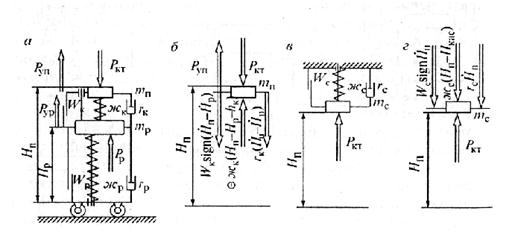
Рис. 13.21. Схемы к определению контактного нажатия для токоприемников с двумя степенями свободы при сосредоточенных параметрах контактной подвески

 

В первом случае получим

Сила жесткости каретки учтена с обратным знаком, так как скобка за ней отрицательна. В этом уравнении все величины получены ранее при решении основного уравнения движения; неизвестным является только Р_кт, которое определяют из формулы

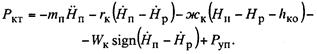
Во втором случае контактное нажатие будет равно:

 

13.8. Методы испытаний контактных подвесок в лабораторных условиях и на полигонах

 

Экспериментальные исследования взаимодействия токоприемника с контактной подвеской целесообразно производить в лабораторных условиях на стендах. При этом можно решать минимум две задачи:

1) варьируя различными характеристиками и конструкциями узлов натурных токоприемников, выявлять их оптимальные варианты или проверять их соответствие техническим заданиям;

2) проверять влияние допущений в используемых методах расчета контактных подвесок и программах для ЭВМ, сопоставляя для этого результаты расчетов и экспериментов на стендах с натурными токоприемниками.

Для исследования параметров токоприемников, влияющих на его вертикальную динамику, можно использовать колебательный стенд, задавая стрелу провеса (амплитуду колебаний) и скорость поезда (частоту колебаний) и принимая подвеску как жесткую с высотным положением в виде синусоиды.

Для исследования параметров и конструкций верхних узлов полозов и кареток в зависимости от вертикальных колебаний проводов и их расположения в плане следует использовать стенд с вращающимся кольцом из проводов.

При испытаниях контактной подвески на полигоне прежде всего разрабатывают программу испытаний в соответствии с поставленными целями, после чего на месте определяют испытательный анкерный участок подвески, измерительные пролеты и опоры для установки датчиков, видеокамер и измерительных шкал, а также уточняют перечень необходимого оборудования и материалов для полевых пунктов. Одновременно согласовывают предоставление «окон» в графике движения для проведения испытаний, а также локомотива с бригадой и испытательных вагонов контактной сети. Для увеличения количества поездок в течение каждого «окна» возможно принятие «челночного» способа движения испытательного поезда по перегону с возвращением на станцию.

Испытательный поезд для исследования контактной подвески формируется из электровоза с требуемой конструктивной скоростью и вагона-лаборатории. Для комплексных автоматизированных измерений параметров контактной сети и некоторых параметров рельсового пути, влияющих на оценку состояния контактной сети, используют вагон-лабораторию контактной сети (ВИКС).

Измерительные пролеты полевого пункта оснащают устройствами для измерения отжатий проводов с изолированного лейтера, пунктами видеосъемок и датчиками экстремальных отжатий в соответствии с описанными выше методиками.

На испытательном поезде определяют статические и динамические характеристики всех токоприемников электровоза и измерительных токоприемников ВИКС.

Проведение статических и динамических испытаний подвески осуществляется согласно программе. Для проведения испытаний задействуют бригады испытателей на электровозе, вагонах-лабораториях и полевых пунктах.

 

13.9. Порядок динамического расчета

компенсированных контактных подвесок

скоростных и высокоскоростных магистралей

 

Расчеты компенсированной подвески предлагается проводить в следующей последовательности (рис. 13.22):

1) особенности конструкции варианта, задаваемые параметры, значения скорости движения поезда и токовых нагрузок;

2) определение погонных нагрузок проводов подвески с учетом заданных метеоданных;

3) определение стрел провеса несущих тросов и контактных проводов для заданных натяжений в нормальном режиме;

4) определение стрел провеса несущих тросов и контактных проводов для заданных натяжений при гололеде;

5) определение длин пролетных струн заданных параметров подвески;

6) определение предварительных провесов рессорных струн при заданных параметрах подвески;

7) определение допустимости ветровых отклонений контактной подвески при заданных параметрах и изменениях натяжений проводов (или допусков);

8) определение жесткости подвески в пролете для заданных параметров подвески;

9) оценка влияния изменений параметров жесткости подвески на критерии ее оптимальности для различных вариантов;

10) проверка вариантов подвески по критическим скоростям и коэффициентам надежности и экономичности;

11) оценка влияния на критерии оптимальности жесткости подвески количества и расположения струн;

12) проверка вариантов количества и расположения струн на критические скорости и коэффициенты надежности и экономичности;

13) выявление оптимального варианта подвески с определенными параметрами;

14) определение для оптимального варианта подвески:

а) стрел провеса несущего троса;

б) длин струн и вспомогательных тросов рессорных струн;

в) коэффициента экономичности;

г) ветровых отклонений;

15) проверка необходимости мероприятий по предотвращению автоколебаний оптимального варианта подвески.

 

 

Предлагаемый порядок работ по созданию подвесок контактной сети для скоростей 250—300 км/ч связан с выбором конструктивных решений и расчетами рациональных статических и динамических характеристик из условий надежного и экономичного взаимодействия с токоприемниками (рис. 13.23). Варианты последовательного выполнения условий подобных методов были разработаны и применены в ОмГУПС при расчете скоростной ПКС постоянного тока КС-200.

 

 

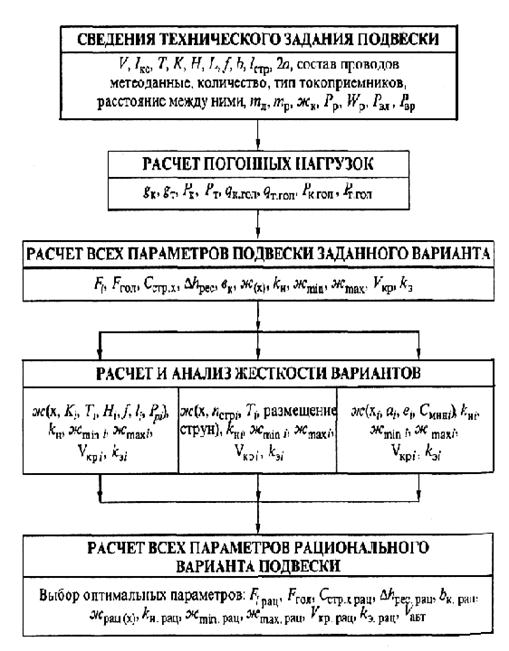
Рис. 13.22. Порядок расчета оптимальных параметров и характеристик скоростной компенсированной цепной контактной подвески

Предлагаемая последовательность расчетов является разделом рассмотренного порядка создания ПКС и базируется на том, что характеристики и параметры современных скоростных ПКС априорно нормированы. К примеру, длина пролета 65 м; рессорный трос от 16 до 22 м; число струн в пролете от 6 до 14 шт.; натяжения проводов и тросов порядка 10—27 кН.

Расчеты компенсированной ПКС предлагается проводить с определением коэффициентов экономичности и надежности; проверок на ветроустойчивосгь и гололед, с учетом параметров токоприемника и т.д.

 

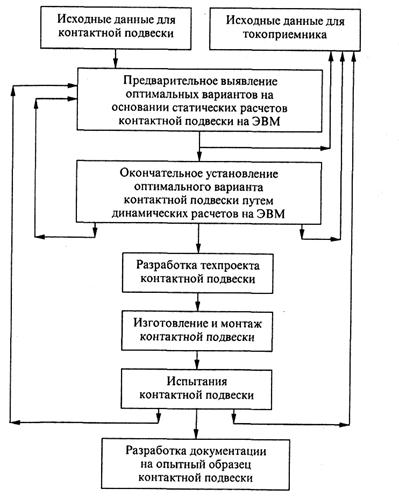
Рис. 13.23. Последовательность работ по созданию контактной подвески для повышенных скоростей движения