13.5. Определение распределенных параметров контактных подвесок

 

Применение сосредоточенных параметров не отражает действительных процессов, имеющих место при токосъеме, так как не принимаются во внимание волновые процессы в проводах при вертикальных колебаниях и двух токоприемниках. С увеличением скоростей движения свыше 200 км/ч использование сосредоточенных параметров нецелесообразно, т.е. необходимо применение подвески с распределенными параметрами по обобщенной расчетной схеме (см. рис. 13.6).

В связи с этим ряд ученых пытались использовать для учета контактной подвески волновые уравнения — дифференциальные уравнения в частных производных. Решение этих уравнений как аналитически, так и численными методами представляет значительные трудности. В целях упрощения решений и повышения достоверности результатов расчетов токосъема предлагается ввести минимальное количество наиболее безобидных допущений, учитывающих только наиболее простые характеристики токосъемных устройств, для которых имеются экспериментальные данные: свободных колебаний проводов H_с(t), траекторий H_л(t), контактных нажатий Р_kт(х), массы m_под, жесткости ж_под, коэффициента вязкого трения r_кп и силы сухого трения W_под подопорных пружинных узлов. При этом, для проведения расчетов использованы обозначения, принятые в п. 13.3 настоящей главы.

Волновые уравнения взаимодействия нескольких токоприемников и контактной подвески. Как указывалось выше, в расчетную схему, используемую для составления уравнений, вводятся некоторые допущения. Так, силы вязкого трения в подвеске принимаются пропорциональными . Жесткость подопорного узла, его масса и т.д. резко возрастают под опорой, поэтому силы, действующие на провода от подпорных узлов и токоприемников, считаются сосредоточенными в точках. Для формализации этого используется функция Дирака , равная 0 при x0 и при x=0. Причем

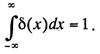                                                                                                            (14.43)

Функция Дирака употребляется для описания плотности единичной массы, силы и т.д., находящейся в точке x=0. Например, плотность силы, вызываемой подопорной жесткостью, есть

                                                                    (13.44)

где H_св — высота точки подвеса при полностью разгруженном подопорным узле (в предположении полной линейности его функции нажатия); l — длина пролета;

n — номер опоры.

Плотность массы от токоприемника, взаимодействующего с контактной подвеской при движении и нахождении его в начальный момент времени t=0 в точке  , равна .

Нажатие рам и вязкое трение в них вводятся в уравнение подобным же образом.

Уравнение движения элементов рассматриваемой системы с несколькими токоприемниками под проводом имеет следующий вид:

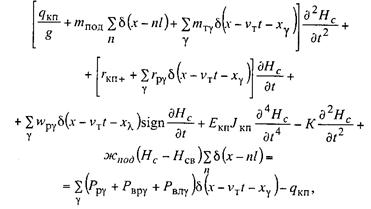                                                  (13.45)

где v_T — скорость движения токоприемника;— координата -го токоприемника при t=0; E_кп J_кп— собственная жесткость проводов; — масса, сила сухого и коэффициент вязкого трения рам, их нажатие и аэродинамические вертикальные силы соответственно для -го токоприемника.

Используя эти волновые уравнения, можно найти кривые свободных колебаний проводов подвески, отыскать траектории полозов и контактные нажатия для одного и нескольких токоприемников (при любом расстоянии между ними).

Уравнение движения элементов рассматриваемой системы выводится из уравнения колебаний струны, которое в общем случае имеет вид

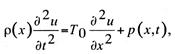                                               (13.46)

где р(х) — линейная плотность струны; Т₀ — сила натяжения, действующая на струну; и — вертикальное перемещение точек струны в момент времени t от положения равновесия; p(x,t) — внешняя сила, действующая на струну.

Уравнение (13.46) имеет бесчисленное множество частных решений. Поэтому одного уравнения недостаточно для полного определения движения струны; нужны еще некоторые дополнительные условия. Так, в начальный момент времени t=0 нужно задать положение и скорость всех точек струны:

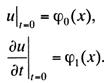                                                                                                            (13.47)

Условия (13.47) называют начальными условиями.

Так как струна ограничена и закреплена, то на ее концах должно быть

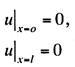                                                     (13.48)

при всяком 0. Условия (13.48) называют краевыми или граничными условиями. Возможны и другие граничные условия.

Итак, физическая задача о колебании струны свелась к математической задаче, где необходимо найти решение уравнения (13.46), удовлетворяющее начальным (13.47) и граничным условиям (13.48).

Определение собственной жесткости различных проводов. Собственная жесткость проводов и тросов, входящая в волновые уравнения, учитывается произведением E_кп,J_кп, которое следует рассчитывать или находить экспериментально. Значения модуля упругости E_кп приводятся в справочниках только для монометаллических проводов, поэтому для сталемедных и сталеалюминевых проводов вопрос осложняется. Для расчета Е_экв комбинированного провода используется следующие выражение:

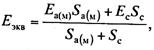                                                (13.49)

где E_а(М) и Е_с — модуль упругости алюминия (меди) и стали соответственно;

S_а(М) и S_С — площадь сечения алюминиевой (медной) части и стальной соответственно.

Моменты инерции сложных сечений контактных проводов определяются по формуле

                                                  (13.50)

где F_i — площадь i-го элемента сечения провода; z_цi— координата центра тяжести

i-го элемента сечения провода; J_i— собственный момент инерции i-го элемента сечения провода.

При этом координаты центра тяжести провода определяются по формуле

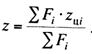                                                     (13.51)

Так как контактный провод имеет неправильную форму в сечении, то для расчета момента инерции контактного провода и определения его координаты центра тяжести необходимо сечение провода разбить на ряд более простых сечений. Тогда площадь сечения сегмента и момент инерции определяется по формулам

                                                (13.52)

где R_i — радиус дуги сегмента;

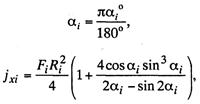                                           (13.54)

где F_i — площадь сечения сегмента.

Выражение для расчета площади сечения трапеции имеет вид:

                                                       (13.55)

где b_i, b₁ — размеры верхнего и нижнего основания соответственно; h_i- — высота трапеции;

                                             (13.56)

где b₀ = b₁-b₁.

Несущий трос, как правило, состоит из нескольких проводов, поэтому для расчета его момента инерции применима формула (13.50), где собственный момент инерции J_xi определяется по выражению

                                                         (13.57)

где d — диаметр провода; F— площадь сечения провода, для круглого провода

                                                          (13.58)

Собственную жесткость различных проводов можно определить экспериментально, нагружая закрепленный одним концом отрезок провода длиной l горизонтальной силой и измеряя его прогиб (рис. 13.18,a). В этом случае собственная жесткость провода будет равна

                                                     (13.59)

 

 

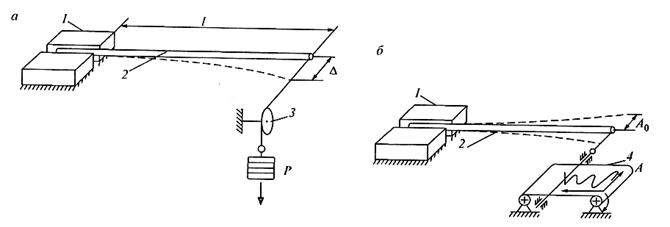
Рис.13.18.Схема экспериментального определения собственной жесткости (а) и коэффициента вязкого трения (б) проводов: 1-неподвижный зажим; 2-провод; 3-блок; 4-самопишущий прибор

 

где Р — сила, действующая на конце провода; l — длина провода;  — прогиб провода.

Коэффициент эквивалентного вязкого трения провода экспериментально определяют по следующей методике (рис. 13.18, б). Один конец отрезка провода закрепляют неподвижно, а другой соединяют с самопишущим прибором, имеющим достаточно высокий класс точности по развертке. Затем, задав начальное отклонение, производят запись виброграммы. Полученную кривую следует обрабатывать одним из методов определения коэффициентов вязкого трения в зависимости от того, какой характер носит демпфирующая сила (линейный или нелинейный). Взяв с виброграммы период амплитуды колебаний и подставив погонный вес провода, найдем

                                                 (13.60)

где q — погонный вес провода;

Т и А_i — период и амплитуда колебаний соответственно.

 

13.6. Косвенные параметры контактных подвесок, взаимодействующих с токоприемниками

 

К группе косвенных параметров можно отнести характеристики, которые могут помочь оценить работу токосъемных устройств без сложных расчетов их взаимодействия на ЭВМ.

К ним относятся: 1) время затухания колебаний подвески t_{с затух}; 2) декремент затухания колебаний подвески D_с; 3) критические скорости подвесок V_с.кр ;

4) коэффициент Доплера подвески _с; 5) линии влияния отжатия (Л ВО) и эластичности (ЛВЭ) подвесок; 6) статические траектории токоприемника H_л(х). Ниже рассмотрены только косвенные параметры критических скоростей и линий влияния отжатия. Остальные параметры достаточно известны из теоретической механики.

Критические скорости. Скорость распространения волны по подвеске, которая должна быть меньше скорости ЭПС, определяется по формуле

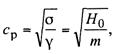                                                (13.61)

где с_р — скорость распространения волны; H₀ — натяжение провода; m — погонная масса провода.

 Коэффициент отражения

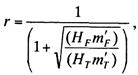                                              (13.62)

где Н_F, m'_F, Н_Т, m'_т— натяжение и масса контактных проводов и несущего троса соответственно.

Скорость движения:

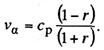                                                  (13.63)

 

 

Коэффициент Доплера

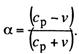                                                     (13.64)

Коэффициент усиления

                                                        (13.65)

Собственные частоты цепных контактных подвесок

                                          (13.67)

 

где  — средняя скорость распространения волны цепной подвески; l — длина пролета;l₁— расстояние до первой нерессорной струны

Оптимальными должны быть приняты параметры, которые обеспечивают наиболее близкий к единице коэффициент неравномерности при нормируемой средней жесткости и скорости волны, меньшей, чем скорость ЭПС.

При анализе КС-200 из условия динамики с параметрами, удовлетворяющими условиям статики, должны анализироваться кривые контактного нажатия в пролете. Среднее его значение должно быть близким к оптимальному из рассмотренной кривой износа. Колебания нажатия не должны быть максимальными, вызывающие подъемы фиксаторов до 200 мм, и минимальными до 20 Н, вызывающими пережоги.

Критические скорости для контактной подвески КС-200 с заданными параметрами оказались для всех трех элементов выше, чем скорость движения предполагаемого ЭПС, — 97 м/с (350км/ч).

Дополнительную проверку на критические скорости высших гармоник проводят по формуле

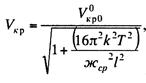                                                    (13.68)

где k —— номер гармоники; Т— натяжение в несущем тросе; ж_cp— средняя жесткость подвески в пролет; l— длина пролета.

Линии влияния эластичности контактной подвески показывают закон изменения подъема контактного провода в рассматриваемой точке при перемещении токоприемника вдоль пролета. Их строят для нажатия токоприемника Р = 1. Кроме того, по этим линиям определяют статический подъем контактных проводов в данной точке при нахождении в пролете двух и более токоприемников.

Линии влияния эластичности контактной подвески в средних частях пролета строят так же, как и линии влияния изгибающего момента простой балки на двух опорах, с той лишь разницей, что ординаты линии влияния делят, кроме того, на величину приведенного натяжения цепной подвески Т+К и измеряют их поэтому в м/кг. Так как приведенное натяжение цепной подвески изменяется в зависимости от температуры, то и линии влияния при таком построении будут получаться различными при разных температурах.

В цепных подвесках с простыми опорными струнами линия влияния имеет треугольную форму с нулевыми ординатами под опорами и с переломом в точке, для которой определяют значения подъема контактных проводов(рис. 13.19,а). Для цепных подвесок, в которых опорные струны находятся на расстоянии с с каждой стороны от оси опоры, принимают, что при перемещении силы Р = 1 под опорой на участке провода между двумя ближайшими от опоры струнами передаваемые на эти струны усилия изменяются по закону прямой. Линия влияния получает при этом вид (рис. 13.19, б) с переломами под ближайшими от опоры струнами и проходит через нуль в точках расположения таких струн в смежных пролетах.

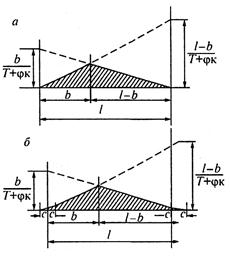
Рис. 13.19. Линии влияния эластичности в пролете цепной подвески с простыми опорными струнами (а) и струнам, смешенными относительно опор (б)