13.3. Обобщенные расчетные схемы токоприемников и контактных подвесок

 

Теоретическое определение траекторий элементов токоприемника и контактного нажатия связано с решением задач динамики (теории колебаний) о движении тел переменной массы под действием разного рода сил. В связи этим первым этапом расчетов является определение в рассматриваемой системе «токоприемник—контактная подвеска» масс, жестокостей, сил сухого и вязкого трения, моментов инерции и установление числа степеней свободы и обоснованный выбор координат.

Обобщенные расчетные схемы токоприемников и контактных подвесок, максимально полно отражающие процесс токосъема и позволяющие получить уравнения, результаты решения которых будут совпадать с результатами экспериментов, составлены на основании рассмотрения конструкции всех узлов современных токоприемников и контактных подвесок как механических систем.

Обобщенная расчетная схема токоприемника была составлена в ОмГУПСе в связи с тем, что известные упрощенные схемы были пригодны для конструкций, созданных в первые годы электрификации.

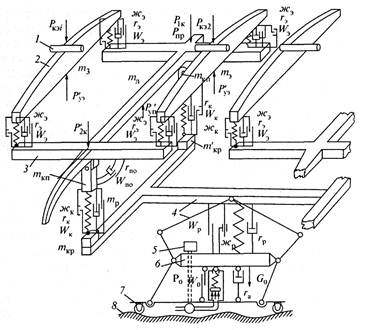
На обобщенной схеме (рис. 13.5) представлен токоприемник с двух каркасным (двойным) полозом положительной кривизны с вторичным подрессориванием, рамного типа, а также с рогами, установленными на раме, не синхронизированными кареткам рычажного типа с нелинейной характеристикой и элементами с сухим и вязким трением, препятствующими повороту полоза вокруг продольной оси.

 

Рис. 13.5. Обобщенная расчетная схема токоприемника: 7 — контактный провод; 2— подрессоренный контактный элемент; 3— полоз с рогами и каретками; 4—авторегулятор основания; 5 — авторегулятор высоты подвижного основания; 6 — подвижное основание; 7— основание на ЭПС; 8 — неровности пути

 

Система подвижных рам токоприемника, имеющая силы сухого трения, установлена на авто регулируемом основании и снабжена гидравлическим демпфером (амортизатором). Статическое нажатие рам зависит от высоты. Крыша кузова совершает вертикальные перемещения. Учтены силы воздействия воздушных потоков на различные элементы токоприемника и силы трения о контактные провода.

Для проведения расчетов вводятся следующие обозначения:

H_под, Н_кас — высота подвеса контактных проводов при отсутствии токоприемника, отсчитываемая от верхней поверхности полозов опущенного токоприемника соответственно под опорой и в любой точке пролета;

H_с, H_э, H_п, Н_p — высота соответственно контактных проводов, верхней поверхности контактных элементов, каркасов полозов, верхнего шарнира системы подвижных рам токоприемника (высоту отсчитывают от верхней поверхности полозов опущенного токоприемника);

H_{куз 0}, Н_куз — высота верхней поверхности полоза опущенного токоприемника над уровнем головок рельсов соответственно на стоянке (т.е. прп отсутствии колебаний кузова) и при движении;

H₀ — расстояние от верхней поверхности полозов авторегулируемого токоприемника при опущенной верхней системе рам (в любом положении подвижного основания) до этой поверхности при полностью сложенном токоприемнике;

m_э, m _{э пp} — масса одного контактного элемента соответственно полная и приведенная;

W_э — сила сухого трения кареток вторичного подрессоривания;

r_э, Р_кэ — соответственно коэффициент и сила вязкого трения кареток вторичного подрессоривания;

ж_э, Р_кэ — соответственно жесткость и функция нажатия вторичного подрессоривания;

 

Р_уэ — вертикальная сила от воздушного потока, действующая на один токосъемный элемент;

m_п, m _{п пp} — полная и приведенная массы полозов;

Р_yп —аэродинамическая подъемная сила полозов;

z— приращение высоты полоза (элемента) за счет кривизны;

m_кп, m_kp — массы частей кареток, скрепленных соответственно с полозом и рамой;

ж_к, Р_к — жесткость пружин и функция нажатия кареток;

r_к, P_дк — коэффициент и сила вязкого трения кареток;

W_К — сила сухого трения кареток;

r_по, w_по — соответственно коэффициент вязкого трения и сила сухого трения при повороте полоза вокруг поперечной оси;

m_p — приведенная масса рам токоприемника;

ж_p — приведенная к верхнему шарниру жесткость подъемных пружин токоприемника;

Р_p — статическое нажатие рам токоприемника с учетом весовой характеристики;

r_p, Р_др — коэффициент и сила вязкого трения подвижных рам;

W_p — сила сухого трения в шарнирах рам;

Р_yp   — аэродинамическая подъемная сила рам;

m₀ — приведенная масса подвижного основания;

W₀ — приведенная сила сухого трения в механизме подвижного основания;

      r₀, R_дО — приведенный коэффициент и сила вязкого трения в системе подвижного основания;

ж₀, T₀ — приведенная жесткость возвратной пружины и опускающая сила основания;

Р_y0— аэродинамическая подъемная сила основания;

Р_кэ ,Р_кт — контактное нажатие соответственно в отдельных точках контакта полозов токоприемника с контактным проводом и полное.

Обобщенная расчетная схема контактной подвески (рис. 13.6) учитывает в общем виде взаимодействие рассмотренных выше элементов для совершенство-вания существующих методов расчета с целью повышения достоверности их результатов. На схеме представлена распределенными параметрами цепная контактная подвеска, состоящая из несущего троса и контактных проводов, имеющих массы, собственные жесткости и внутреннее вязкое трение. Струны приняты нелинейно-эластичными как под опорой, так и в средней части пролета с элементами, создающими силы сухого и вязкого трения (демпферами). Подопорный узел (крепление несущего троса к поддерживающему устройству) принят пружинным. Учтены сосредоточенные массы на проводе под опорой. Подвеска объемная, расположение ее контактных проводов в плане задается около опор фиксирующими устройствами. Для проведения расчетов вводятся следующие обозначения:

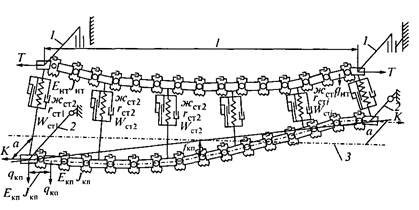
Рис. 13.6. Обобщенная расчетная схема контактной подвески: 1 — консоль; 2 — фиксатор; 3 — ось пути, l — длина пролета; а — зигзаг; f— стрела провеса провода; Т— натяжение троса; К—натяжение контактного провода

 

      К — натяжение контактного провода;

     q_кп — погонная масса контактного провода;

     J_кп — момент инерции сечения контактного провода;

     E_кп — модуль упругости контактного провода;

     r_кп—коэффициент внутреннего вязкого трения контактного провода;

q_нт — погонная масса несущего троса;

Т— натяжение несущего троса;

          J_нт — момент инерции сечения несущего троса;

Е_нт — модуль упругости несущего троса;

r_нт — коэффициент внутреннего вязкого трения несущего троса;

ж_ст, Р_ст — жесткость и функция нажатия струны;

r_ст, Р_дст — соответственно коэффициент и сила вязкого трения в демпферах струн;

W_ст — сила сухого трения в демпферах струн;

m_под, W_под — сосредоточенная масса и сила сухого трения подопорного узла;

ж_под, Р_под — жесткость и функция нажатия подопорного узла;

ж _{к уд} — ударная жесткость контактного провода;

r_под, P _{д под} — коэффициент и сила вязкого трения подопорного узла;

F — стрела провеса несущего троса;

f— стрела провеса контактного провода;

а — зигзаг контактного провода.

Основные методы, которые можно рекомендовать для применения при расчетах взаимодействия, должны быть точными, с использованием ЭВМ. Приближенные расчеты по упрощенным методам можно проводить лишь для анализа работы или усовершенствования конструкций в условиях депо или участков энергоснабжения.

Методы расчетов можно классифицировать по числу степеней свободы у токоприемника и способу представления контактной подвески (с сосредоточенными или распределенными параметрами).

 

13.4. Сосредоточенные параметры контактных подвесок и их определение

 

Сосредоточенные параметры включают в себя следующие характеристики контактных подвесок в пролетах, входящие в расчетные схемы (И.И. Власов, А.В. Фрайфельд): 1) высотное положение при отсутствии токоприемника; 2) жесткость (эластичность); 3) приведенная масса; 4) сила сухого трения; 5) коэффициент вязкого трения.

Перечисленные параметры используются в качестве исходного массива данных по контактной подвеске для расчета по описываемой ниже методике. От тщательности расчета или экспериментального определения параметров зависит достоверность получаемых траекторий полоза, рам токоприемника, а также контактного нажатия.

Высотное положение проводов простых и цепных подвесок. Эпюра высотного положения проводов определяется экспериментально путем прямых измерений с изолированной съемной вышки (лейтера) относительно уровня головки рельсов в различных точках пролета (под струнами и в середине между ними), начиная от опоры. Эта же эпюра может быть определена расчетно относительно горизонтальной оси на уровне головки рельсов. Формулы для расчета были приведены в гл.З. Для случая упрощенного определения стрелы провеса простой контактной подвески (когда пересечение осей координат взято относительно опоры):

где H_пoд — высота провода под опорой.

Для цепной контактной подвески высотное положение определяется аналогичным способом, но с учетом стрел провеса несущего троса. Для полукомпенсированной подвески с простыми подпорными струнами высотное положение изменяется в течение года. При этом кривая зависимости высотного положения от температуры выглядит как парабола выгнутая вниз при положи-тельных температурах и вверх при отрицательных, а при температуре беспровесного положения — в виде прямой линии. Для полукомпенсированной подвески с рессорными струнами на эпюре от опоры до первой нерессорной струны появля-ются горизонтальные площадки. Влияние температуры аналогично рассмотренному выше. Для полностью компенсированной подвески высотное положение постоянно.

Для типовой компенсированной подвески стрела провеса задается равной 60 мм, соответственно выглядит и эпюра. Для современных скоростных подвесок провод регулируется на стрелу провеса, равную нулю, например, в контактной подвеске КС-200. Точные расчеты высотных положений проводов подвески следует проводить на ЭВМ (например, с учетом конечного числа струн).

Жесткость подвески представляет собой отношение силы, поднимающей провода, к величине этого подъема. Обратная величина жесткости—эластичность подвески—величина подъема провода под действием единичной силы, направлен-ной снизу вверх и действующей в данной точке. Экспериментальное определение жесткости производят со съемной вышки (лейтера) или площадки дрезины. Возможна запись аппаратурой вагона-лаборатории сначала высотного положения проводов, а затем траектории полоза при заданном нажатии токоприем-ника и движении поезда с малой скоростью. Частное от деления нажатия на разность траектории и высотного положения дает эпюру жесткости.

Более точные результаты измерения получаются вручную установленной на лейтере простой стойкой с блоком, тарированными грузами и линейкой. При этом функция нажатия подвески имитируется грузами и измеряется по линейке. Кроме того, может быть установлена линейность характеристики, а также определена величина силы сухого трения как разность ординат измеренной кривой при нагру-женном состоянии и без нагрузки. Под опорой функция нажатия измеряется при Действии силы, направленной сверху вниз для оценки способности подвески гасить колебания после прохода токоприемника (ЭПС).

При проектировании новых контактных подвесок целесообразно коэффициент неравномерности представлять как отношение максимальной жесткости в пролете к минимальной. В расчетах можно использовать параметры эластичности, затем брать обратные ей величины жесткости.

В следующих разделах приведены выводы формул и уравнений для расчетов простой подвески, подвески на сплошном основании, для цепной (в средней части пролета, подопорной зоне, межструновом пролете и с учетом разгрузки струн). Выводы выполнены методом И.И. Власова как наиболее простым и логичным. При необходимости получения более точных результатов можно использовать уравнения К.Г. Марквардта, а также методы расчетов, разработанные в УрГУПСе (А.В. Ефимов и др.) и ОмГУПСе (В.И. Себелев и др.). Последние учитывают максимальное число факторов, но очень трудоемки при обязательном расчете по программам на ЭВМ.

Расчет жесткости (эластичности) простых и цепных подвесок. Точный расчет эластичности представляет значительные трудности, приближенные же ее значения могут быть легко найдены, если принять ряд допущений, позволяющих применить упрощенные методы расчета. В первом приближении при статическом приложении сил можно принять, что натяжение проводов остается неизменным, и не учитывать жесткости проводов. Постоянное натяжение проводов вполне допустимо для компенсированных контактных проводов, а также и некомпенсированных несущих тросов при подвесных изоляторах и поворотных или полуповоротных консолях. Примем также, что сила нажатия Р токоприемника невелика по сравнению с основной нагрузкой, равномерно распределенной на контактную подвеску.

Рассмотрим случай простой контактной подвески с жесткими опорными точками (рис. 13.7). Действие вертикальной силы Р, приложенной на расстоянии х от левой опоры, вызывает подъем контактного провода на высоту  и разгрузку опор. Так как после приложения силы Р часть пролета, представленная на рисунке, остается в равновесии, сумма моментов действующих сил относительно точки приложения силы Р должна равняться нулю:

 

где Р(l-х)/l  представляет уменьшение левой опорной реакции, вызванное приложением силы Р.

 

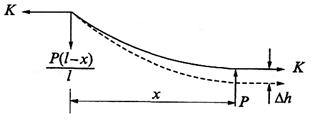
Рис.13.7. Схема для определения отжатия провода простой контактной подвески

 

Решая уравнение (13.11) относительно , получим

Значение эластичности контактной подвески  в точке, расположенной на расстоянии х от левой опоры, определим по формуле

При расположении силы Р в середине пролета (при x = l/2)

получим

Отсюда график эластичности простой контактной подвески при жестких опорах выражается параболой, имеющей ординатув середине пролета и нулевые ординаты под опорами.

Если контактный провод подвешен на часто расположенных гибких струнах к какой-либо неэластичной конструкции, как показано на рис. 13.8, то подъем контактного провода в точке приложения силы Р может быть представлен выражением

и сила Р уравновешивается весом поднятого на длине с контактного провода. Подставляя Р =g_кс в это выражение, получим

 

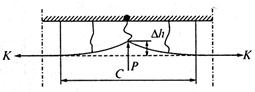
Рис. 13.8. Схема для определения отжатия контактного провода, подвешенного на струнах к жесткой конструкции

 

При цепной контактной подвеске сила Р, приложенная в средней части пролета, вызывает подъем как контактного провода, так и несущего троса.

Рассматривая часть пролета цепной подвески с простыми опорными струнами (рис. 13.9), где конструктивный коэффициент цепной подвески = 1, и приравнивая к нулю сумму моментов всех сил относительно точки А, получим уравнение

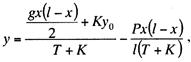
решая которое относительно у, установим, что

 

где у₀ — ордината несущего троса в рассматриваемой точке пролета при беспровес-ном положении контактного провода.

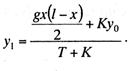
При отсутствии силы Р ордината у₁ несущего троса определится выражением

 

Рис. 13.9. Схема для определения отжатия контактного провода цепной подвески

 

Вычитая выражение (13.15) из (13.16), находим  — отжатие цепной подвески под действием силы Р:

 

Разделив на Р, получим значение эластичности цепной под-вески в данной точке пролета:

                                             (13.18)

Для точки, расположенной в середине пролета (при х =l/2)

                                               (13.19)

В рессорных цепных подвесках вследствие вызываемых рессорной струной изменений высоты контактного провода под опорой момент пары сил К в выражении (13.14) вместо К (у -у₀) будет равен (у -у₀).

Выражения (13.18) и (13.19) получат при этом вид

                                                  (13.20)

                                                  (13.21)

При расположении силы Р между струнами к значению эластичности, определяемому выражением (13.20), необходимо добавить эластичность контактного провода в междуструновом пролете, которая определяется в зависимости от расстояния между струнами и от положения силы Р по формуле

где а — расстояние между струнами; — расстояние от левой струны.

 Формулы (13.17) — (13.20) справедливы для случая, когда воздействие силы Р на цепную подвеску не вызывает разгрузки струн, т.е. пока Р < R_стр, где R_стр —реакция струны, которая при расстоянии между струнами а может быть определена из выражения

                                                (13.22)

При Р > R_стр произойдет дополнительный подъем контактного провода, который согласно (13.13) можно приближенно определить из выражения, которое получено из условия, что вес поднятого контактного провода  равен силе (Р- R_стр ), вызвавшей этот подъем:

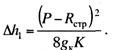
В частях пролета, прилегающих к опорам, эластичность контактной подвески может изменяться в широких пределах в зависимости от конструкции опорного узла. В цепных подвесках с простыми опорными струнами подъем контактного провода под действием силы Р вызывает лишь разгрузку опорных струн и происходит в значительной своей части независимо от несущего троса.

Разберем сначала случай, когда фиксатор отсутствует, а контактный провод направлен по оси прямого пути и располагается в пролете беспровесно (f_k = 0). Рассмотрим отрезок АВ контактного провода (рис. 13.10), составляющий два междуструновых пролета и подвешенный на трех гибких струнах. Средняя струна крепится к седлу несущего троса и, следовательно, не обладает эластичностью; крайние струны крепятся к несущему тросу на расстоянии с от опоры. Приложение силы Р в точке С вызывает разгрузку средней струны и подъем этой точки на, относительно уровня расположения точек подвеса контактного провода на смежных струнах. Величину подъема , определим по формуле, выведенной для свободно подвешенного провода, точки крепления которого расположены на различной высоте, откуда для принятых (рис. 13.10 и 13.11) обозначений получим

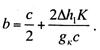
Так как Р=2g_kb, то из предыдущего выражения имеем

Назовем через R_стр начальную реакцию струны (до приложения силы Р) и через Р_s = Р - R_стр   — избыточную силу, вызывающую подъем контактного провода под опорной струной.

 

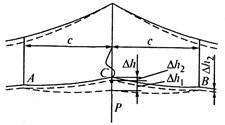
Рис. 13.10. Схема изменений положения проводов цепной подвески при отжатии контактного провода силой, приложенной под опорной струной

 

Так как в данном случае R_стр = g_kс , то

 

откуда

Подъем контактного провода под опорной струной (см. рис. 13.10) вызывает также разгрузку несущего троса в пролете и, следовательно, некоторый дополнительный подъем как несущего троса, так и рассматриваемого отрезка АВ контактного провода. Можно принять, что разгрузка цепной подвески в прилегающих к рассматриваемой опоре пролетах происходит под действием сосредоточенных сил, приложенных в точках А и B где расположены первые пролетные cтруны.

 

Рис. 13.11. Схема для расчета подъема контактного провода под действием силы, приложенной под опорной струной

 

Тогда подъем   проводов цепной   подвески каждой из этих точек под действием  разгружающих сил  можем определить по общей формуле для цепной подвески (13.17) как

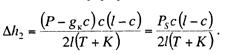
Общий подъем контактного провода под действием силы Р, приложенной под опорной струной (см. рис. 13.11), определится выражением

которое после преобразовании примет вид

                                                                                            (13.23)

Рассмотрим теперь общий случай, когда имеется фиксатор, подвешенный на опорной струне к седлу несущего троса, и контактный провод располагается в смежных пролетах со стрелой провеса f_к. При отсутствии силы Р (рис. 13.12) реакция опорной струны определяется выражением

                                             (13.24)

где Q_ф — передающаяся на опорную струну часть веса фиксатора; H_ф—горизонтальная составляющая реакции фиксатора; d — расстояние по горизонтали от фиксирующего зажима до шарнира фиксатора; h — расстояние по вертикали от шарнира фиксатора до уровня контактного провода в месте крепления к нему фиксатора; Q_к — передающаяся на опорную струну часть веса контактного провода, определяемая в соответствии с (13.22) выражением

 

             

 

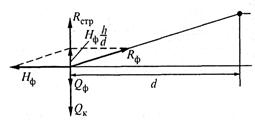
Рис. 13.12. Схема разложения сил в точке крепления фиксатора к контактному проводу

Верхние знаки в формуле (13.24), как и в формулах, следующих ниже, относятся к растянутым фиксаторам, нижние — к сжатым. Если правая часть уравнения (13.24) обращается в нуль, то силы, приложенные в опорном узле контактного провода, взаимно уравновешиваются и реакция опорной струны становится равной нулю. Если правая часть уравнения (13.24) получит отрицательное значение, что может произойти при растянутом фиксаторе и больших отрицательных стрелах провеса контактного провода, то равновесие нарушится и точка крепления контактного провода у фиксатора поднимется на величину  (рис. 13.13), в результате чего вновь будет достигнуто равновесие. При этом вертикальная составляющая  реакции   фиксатора  примет   новое  значение  и возникнет вертикально направленная вниз сила Q_s=Р_s, величину которой можно определить, пользуясь выражением (13.23):

                                                                                              (13.25)

 

которое может быть приведено к виду

где

 

 

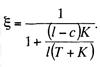
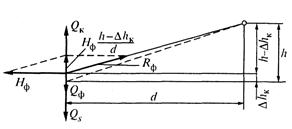
Рис. 13.13. Схема разложения сил в точке крепления фиксатора к контактному проводу при разгрузке струны и подъеме контактного провода

 

Уравнение (13.14) примет при этом следующий вид:

откуда

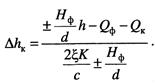                                         (13.26)

Если к контактному проводу в месте крепления к нему фиксатора будет приложена вертикально направленная вверх сила Р, то возможны два случая.

1. При Р  R_стр произойдет частичная или полная разгрузка опорной струны и подъема провода не будет (= 0). Новая реакция струны R_стр ' определится в этом случае из выражения

                                                                                              (13.27)

2. При Р > R_стр (рис. 13.14) произойдет полная разгрузка струны и подъем контактного провода на высоту, которая, подобно предыдущему, может быть найдена из уравнения

получаемого из условия равновесия сил, приложенных в опорной точке контактного провода. Решая это уравнение относительно, получим

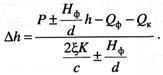                                                                                               (13.28)

 

 

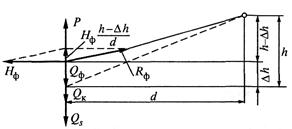
Рис. 13.14. Схема разложения сил в точке крепления фиксатора к контактному проводу при отжатии фиксатора силой Р

Ввиду наличия неэластичной опорной струны  не может иметь отрица-тельных значений. Поэтому, если правая часть уравнения (13.28) получится отрицательной, это покажет, что опорная струна при воздействии силы Р не разгружается и подъема контактного провода не происходит. Реакцию опорной струны можно в этом случае определить из уравнения (13.27).

Эластичность контактной подвески под опорой определяется выражением

В этом случае эластичность не остается постоянной  и  независимой от Р, как это имеет место в пролете. При  эластичность = 0, при  эластичность возрастает с увеличением Р. Если до приложения силы  Р  контактный провод под  опорой был уже приподнят на  под действием сил Q_k и H_Ф эластичность надо определить по формуле

где — общий подъем контактного провода под опорой при воздействии на провод силы Р, определяемый по формуле (13.28); _к — подъем контактного провода под опорой при отсутствии силы Р, определяемый по формуле (13.26). Вычитая выражение (13.26) из выражения (13.28), получим

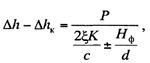
откуда

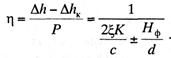
В том случае, если фиксатор не подвешивается на струне и ближайшие струны располагаются на расстоянии с с обеих сторон от него, к контактному проводу в точке крепления фиксатора будут приложены вертикальные силы и

(рис. 13.15). Если эти силы взаимно не уравновешиваются, то происходит поворот фиксатора и подъем или опускание контактного провода на высоту _{к ,} вследствие чего появляется уравновешивающая сила Q_s, величина которой в соответствии с формулой (13.25) может быть определена из выражения

 

 

Рис. 13.15. Схема разложения сил в точке крепления фиксатора к контактному проводу и изменения положения фиксатора при отсутствии опорной струны

 

 которое может быть приведено к виду

где                                                                                              (13.29)

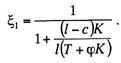                                                                                                        (13.30)

Высота подъема _к может быть определена по формуле

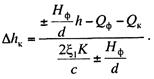
В отличие от предыдущего величина _к в зависимости от соотношения сил может получать как положительные, так и отрицательные значения. В последнем случае контактный провод на участке между ближайшими от фиксатора струнами будет получать прогиб вниз и нагрузка, создаваемая фиксатором, будет передаваться на эти струны. При положительных значениях А//к контактный провод на этом участке будет иметь выгиб вверх, благодаря чему смежные с опорой струны будут частично, а в некоторых случаях и полностью разгружаться. Эластичность контактной подвески в точке крепления фиксатора может быть определена в этом случае по формуле

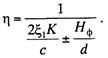
В рессорных цепных подвесках эластичность опорных точек в значительной степени определяется пружинящим действием рессорного троса. Рассмотрим, как изменяется в этом случае положение опорной точки контактного провода под действием приложенной к ней и направленной снизу вверх вертикальной силы Р. Как и ранее, будем предполагать, что пршюжение силы Р не вызывает изменения натяжения несущего троса на данном анкерном участке.

Рассмотрим (рис. 13.16) схему опорного узла рессорной цепной подвески с действующими в нем силами. Делая сечения по ЕF и МN и приравнивая к нулю суммы моментов относительно точки А сил, приложенных к отсеченным частям, получим

                                                                                                               (13.31)

                                                                                                (13.32)

Ввиду малости углов  и  можно принять

Тогда, складывая выражения (13.31) и (13.32), получим

 

Рис. 13.16. Схема для определения натяжений проводов в опорном узле рессорной цепной подвески

 

Полагая, что

                                                                                                       (13.33)

получим выражение

                                                                        (13.34)

Так как К₁ + К₂ = 1, выражение (13.34) приводится к виду

                                                                                                            (13.35)

Без существенного ущерба для точности расчета можно принять, что значения К₁  и К₂ остаются без изменений при различных значениях b. Тогда в выражении (13.35) величина b будет определяться лишь изменениями силы Q.

Для различных значений силы Q₁ и Q>₂ можно написать

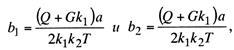
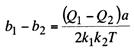
                                                                                                               (13.35)

где  — изменение вертикальной силы Q вызванное воздействием силы Р и определяемое выражением

                                                                                                     (13.37)

Здесь второй член ± представляет реакцию фиксатора, вызванную подъемом его на высоту , а третий член Q_s-реакцию, вызванную подъемом контактного провода под рессорной струной относительно уровня крепления контактного провода на ближайших от опоры простых струнах. Так как подъем несущего троса в точках A и С(рис. 13.17) вызывает близкие по величине подъемы троса в точках Е и F, можно приближенно принять, что подъем контактного провода, вызывающий появление реакции Q_s, определяется лишь изменением стрелы провеса вспомогательного провода .

Полагая ₁и ₂ пропорциональными значениям и у, а следовательно, и значениям К₁и К₂ получим для реакции Q_s согласно (13.29) и (13.30) следующее выражение:

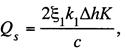                                                                                                       (13.38)

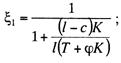
с — расстояние от опоры до ближайшей простой струны.

Тогда выражение (13.36)   после  подстановки в него значений (13.37) и (13.38) получит вид

 

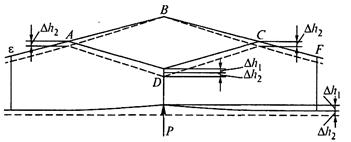
Рис. 13.17. Схема для определения отжатия контактного провода в опорном узле рессорной цепной подвески

 

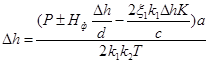                                                                                                 (13.39)

Решая уравнение (13.39) относительно, получим

                                                                             

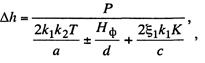
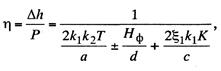                                                                              (13.40)

Это выражение дает возможность определить эластичность контактной подвески под рессорной струной в зависимости от принятых параметров цепной подвески и рессорной струны.

Приведенная масса подвесок. Масса контактной подвески распределена вдоль линии и в уравнениях, в которых подвеска рассматривается в виде системы с распределенными параметрами, учитывается общей плотностью проводов, составляющих цепную подвеску.

Рассматривая контактную подвеску в виде дискретной системы для заданного интервала отсчета, вводят понятие приведенной массы подвески m_к. Так как это понятие является условным, важно правильно представлять физический смысл приведенной массы в соответствии с принятой расчетной схемой. Кроме того, точность результатов теоретических исследований может зависеть от значения и характера изменения этой массы вдоль пролетов, подвески. Если рассматривать условную массу подвески при свободных колебаниях, то закон ее изменения вдоль пролета характеризуется кривой; максимальное значение массы имеет место у опор. Если же считать, что условная масса подвески имеет в точке контакта с токоприемником такую же скорость, что и контактный провод, и запас кинетической энергии, равный запасу энергии реальной контактной подвески во всем пролете, то максимальное значение массы будет в середине пролета. При этом в первом случае масса у опор будет в несколько раз больше, чем в середине пролета, а во втором случае — на 10—20% меньше. Результаты расчетов по формулам, основанным на различной физической сущности условной массы, определяют ее значение, отличающееся в отдельных случаях для одних и тех же условий в несколько раз.

Из экспериментальных данных следует, что значения условных масс мало изменяются вдоль пролетов и немного возрастают с увеличением скоростей движения и числа контактных проводов. Расчеты, проведенные на ЭВМ, показали, что нет необходимости при теоретических исследованиях учитывать изменение массы m_к. Оказалось, что при принятых схемах замещения допустимо принимать усредненные значения m_к неизменными вдоль пролета и равными 30 кг для одинарных контактных подвесок с одним контактным проводом и 40 кг с двумя контактными проводами. Справедливость этого вывода подтверждена сходимостью расчетов, выполняемых для указанных значений m_к, с опытными данными.

Наиболее достоверный результат для незначительных скоростей движения может быть получен по рекомендации И.И. Власова. Среднее значение расчетной массы контактной подвески m_с за период t₂, которое определяется при подъеме контактного провода по выражению для пассивного нажатия рам токоприемника, будет равно

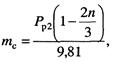                                                                                                            (13.41)

где n — коэффициент скорости, который может быть принят равным нулю, при ее малых значениях.

Коэффициент вязкого и сила сухого трения. Демпфирующая характеристика контактной подвески может в значительной мере повлиять на качество токосъема, а также на колебания подвески под действием ветровой нагрузки в таком сложном режиме, каким являются автоколебания. Разрабатывая новые контактные подвески и сравнивая их с известными конструкциями, обычно пользуются логарифмическим декрементом колебаний подвесок:

                                                                                                            (13.42)

где A_ki и А_ki+1 — два последовательных максимальных отклонения системы.

Этот показатель является полезным лишь для качественной оценки сравниваемых конструкций, причем в таких режимах их работы, как затухание колебаний подвески до и после прохода токоприемников или при автоколебаниях. Подробные исследования характеристик рассеивания энергии (диссипативных) отечественных контактных подвесок показали, что скорость и характер процесса затухания колебаний подвесок около положения статического равновесия зависят от вида упругой характеристики подвески, начальной амплитуды колебаний проводов и зоны пролета.

На процесс колебаний около положения статического равновесия контактного провода, особенно в зоне опорного узла, оказывают влияние рессорные и простые струны, ограничивающие вертикальные перемещения провода. Исследованиями установлено, что с увеличением нелинейности упругой характеристики контактной подвески при повышении жесткости в зоне отрицательных перемещений контактного провода поглощение энергии возрастает.

При различных амплитудах колебания контактного провода превалирующими можно считать различные виды трения: диссипация при А_ki> 0,15 0,20 м вызывается главным образом силами турбулентного трения; при А_ki = 0,03  0,15 м — силами вязкого трения, а при А_ki < 0,03 м — силами сухого трения. Известно также, что наибольшая диссипация энергии происходит в опорной зоне, наименьшая — в середине пролета. Уменьшение жесткости ж_с около опор при использовании рессорных проводов, пружин и других устройств, как правило, приводит к ухудшению демпфирующих характеристик подвесок. Поэтому, добиваясь уменьшения жесткости подвесок около опор, необходимо принять эффективные меры по увеличению диссипации энергии в этой зоне (в частности, этого можно добиться установкой дополнительных струн, ограничивающих перемещение провода ниже положения равновесия).