11.3. Ветровые отклонения проводов и допустимые длины пролетов

простых контактных подвесок и ЛЭП

 

Величина горизонтального отклонения провода при простой подвеске легко может быть определена на основании ранее выве­денных соотношений.

При действии на провод вертикальной g и горизонтальной р_к нагрузок, провод расположится в наклонной плоскости, как показано на рис. 11.3, где дан поперечный разрез провода в пролете.

Обозначив через Ь_к величину горизонтального отклонения провода в данной точке и через у провес провода в этой точке в направлении результирующей силы q, из подобия треугольников получим

                                                                           (11.1)

Величина провеса провода в любой точке пролета согласно (3,24) может быть опреде­лена выражением

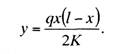
Подставив это значение y выражение (11.1), получим:

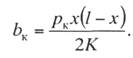                                                                                                               (11.2)

Для средней точки пролета, где стреле про­веса провода f будет соответствовать наи­большее горизонтальное отклонение прово­да b_{к max} из выражения (11.2) получим

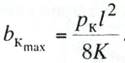                                                                                             (11.3)

При зигзагообразном расположении контактного провода откло­нение его от оси пути будет определяться суммой отклонений у₁ и у₂ (рис. 11.4), величины которых могут быть найдены из выражений

    

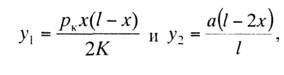
где а — величина зигзага провода.

 

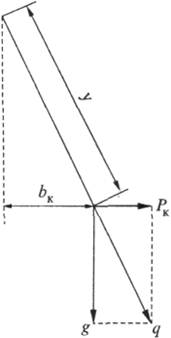
Рис. 11.3. Схема располо­жения провода при откло­нении его ветром

 

 

Рис. 11.4. Схема расположения отклоненного ветром провода на прямой при главных зигзагах: 1 — ось пути и токоприемника; 2,3 — неотклоненное и отклоненное положение контактного провода; 4 — опора

Отсюда получим значение отклонения провода b_к от оси пути в любой точке пролета, расположенной на расстоянии x от опоры:

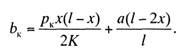                                                                                            (11.4)

Приравнивая к нулю первую производную Ь_к и определяя из получен­ного уравнения значение л; находим расстояние от опоры, при кото­ром отклонение контактного провода от оси пути будет наибольшим:

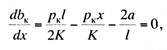
откуда

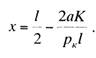
После подстановки этого значения х в выражение (11.3) получим

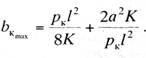                                                                                             (11.5) 

В том случае, если провод имеет различные зигзаги а₁ и а₂, величи­на наибольшего его отклонения определится следующим образом. Обозначим через а среднюю величину зигзага контактного провода:

                         

тогда согласно рис. 11.5 получим:

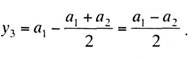                                                                                    (11.6)

Величина наибольшего отклонения провода в пролете может быть определена при этом согласно (11.5) и (11.6) из выражения

                                   (11.7)

Если в выражении (11.5) положить b_{к max} = b_{к доп} и решить это уравнение относительно l, то получим выражение для определе­ния наибольшего пролета провода на прямых участках при дан­ных р_к, а, К и b_{к доп}

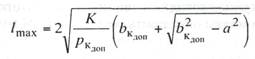                                                                                 (11.8)

 

 

Рис. 11.5. Схема расположения отклоненного ветром провода на прямой при неравных зигзагах: 1 — ось пути и токоприемника; 2 — неотклоненный про­вод; 3 — отклоненный ветром провод; 4 — опора

 

На кривых участках вынос контактного провода выполняется в одну и ту же сторону от оси пути на обеих опорах, ограничива­ющих участок кривой. При отклонении провода ветром на кри­вой он занимает положение, показанное на рис. 11.6.

Величина стрелки кривой оси пути у_х может быть определена из схемы, представленной на рис. 11.7.

Из прямоугольного треугольника ABC имеем:

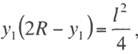
откуда получим:

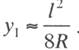
Величина отклонения провода от оси пути у₂ при отсутствии вет­ра определится как (см. рис. 11.6)

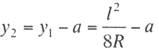                                                                                  (11.9)

 

 

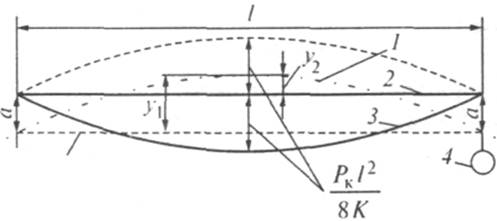
Рис. 11.6. Схема расположения отклоненного ветром провода на кривой: 1 — ось пути и токоприемника; 2 — неотклоненный провод; 3 — отклоненный вет­ром провод; 4 — опора; 5— хорда кривой пути

 

При действии ветра на провод величину наибольшего отклонения про­вода от оси пути можем определить согласно рис. 11.6 из выражения

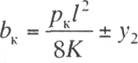
где знак плюс соответствует направле­нию ветра внутрь кривой, а знак ми­нус — на внешнюю сторону кривой. Наибольшее отклонение провода от оси токоприемника получается в этом случае при ветре, направленном внутрь кривой, и оно равно

откуда после подстановки значения y₂ из  выражения (11.9) получим

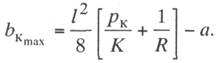                                                                       (11.10)

Значения наибольших допускаемых пролетов на кривых участ­ках пути получим, приняв в выражении (11.10) b_{к max} = b_{к доп} и ре­шив его относительно l_max.

После несложных преобразований получим:

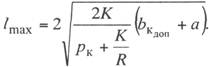                                                                       (11.11)

На кривых больших радиусов значения l_max по формуле (11.11) при нормальных выносах провода у опор получаются больше про­лета l_max, определенного по формуле (11.8) для прямых участков. Однако в практике проектирования ограничивают длину проле­тов на таких кривых наибольшей длиной пролета, установленной для прямых участков, исходя из которой определены габаритные размеры опор и размещение на них поддерживающих устройств. Величину выносов провода a₁ у опор в таких случаях определяют из условия, чтобы провод в середине пролета располагался по оси токоприемника. Как видно из рис. 11.6, это будет тогда, когда

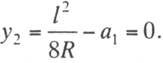
Решая это уравнение относительно a₁, получим

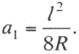                                                                                                           (11.12)

 

 

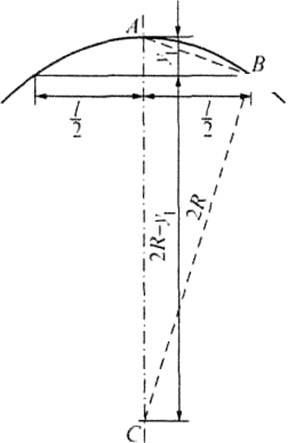
Рис. 11.7. Схема для опреде­ления стрелки кривой пути

Все приведенные выше выражения были выведены без учета сме­щений точек крепления провода на опорах при ветре (вследствие про­гиба опор и пр.). Но если обозначить величину этих смещений через у, приведенные выше формулы примут вид:

– для прямых участков при расположении контактного провода с зигзагом а

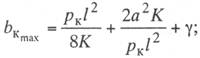                                                                                   (11.13)

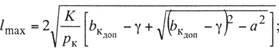                                                                (11.14)

– для кривых участков

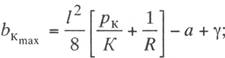                                                                           (11.15)

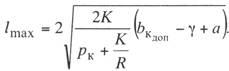                                                                       (11.16)

 

11.4.      Ветровые отклонения проводов и допустимые длины пролетов

цепных контактных подвесок

 

В цепной подвеске отклонение контактных проводов определя­ется с учетом влияния несущего троса, на который действует нагруз­ка р_т . При различных отклонениях несущего троса и контактного провода струны принимают наклонное положение в перпендикуляр­ной оси пути плоскости и передают часть ветровой нагрузки с троса на контактный провод или обратно (в зависимости от того, какой из этих проводов имеет большее горизонтальное отклонение).

Точный учет взаимодействия несущего троса и контактного провода при ветровом отклонении представляет значительные трудности. Ниже приводится вывод приближенных формул для ветрового расчета цепной подвески, основанных на сравнительно простых допущениях и дающих в то же время вполне достаточную для практических целей степень точности.

В качестве основного допущения принимается, что контактный про­вод и несущий трос взаимодействуют между собой (в отношении пере­распределения между ними ветровой нагрузки) лишь в средней части пролета, равной половине общей его длины. Нагрузка, передающаяся с контактного провода на несущий трос (или обратно), принимается на этом участке пролета равномерно распределенной.

Если принять длину струн в этой части пролета постоянной и рав­ной среднему ее значению, то принятое допущение является равносиль­ным тому, что все струны в средней части пролета имеют при ветре одинаковый угол наклона (в направлении поперек пути) и разность ветровых отклонений контактного провода и несущего троса остается в этой части пролета неизменной. Тогда для какого-либо поперечного сечения подвески в средней части пролета (рис. 11.8) можно написать:

где е — разность отклонений контактного провода и несущего троса в средней части пролета;

      р'— равномерно распределенная нагрузка в сред­ней части пролета, передающаяся с контактного провода на несущий трос (или обратно);

     g_K — нагрузка от веса контактного провода;

      с' — расстояние по вертикали от контактного провода до несущего троса.

В дальнейшем ввиду относительно малых значений угла накло­на струн к вертикали принимаем с' равным средней длине струны С, т.е. полагаем, что

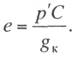                                                                                                      (11.17)

Среднюю длину струны в средней части пролета, равной половине общей его длины, оп­ределим из выражения

                                                                                            (11.18)

где С_т — длина струны в сере­дине выбранного пролета;

       F₀ — стрела провеса несущего троса при беспровесном положении контактного провода.

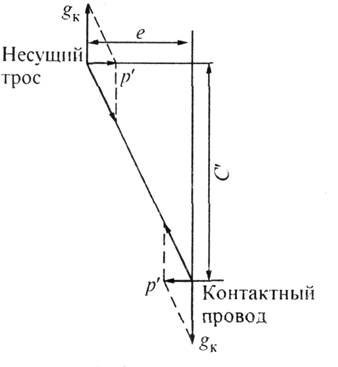
Рис. 11.8. Схема приложения на­грузок к проводам цепной подвес­ки, отклоненной ветром

 

В зависимости от конструк­тивной высоты цепной подвес­ки h величина С определяется выражением

                                                                (11.19)

Величину горизонтального отклонения несущего троса b’_T  под действием равномерно распределенной нагрузки р', приложенной на среднем участке пролета длиной l/2 (рис. 11.9), определим из выражения

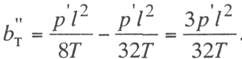                                                                        (11.20)  

Обозначим через р_э величину эквивалентной удельной нагруз­ки, передающейся с контактного провода на несущий трос, рас­пределенной равномерно по длине всего пролета l и вызывающей ту же стрелу провеса  b”_T.

Тогда

откуда

                                                                                                      (11.21)

Значения полного горизонтального отклонения несущего тро­са  b’_T  и контактного провода b_к в середине пролета могут быть определены при этом по формулам

 

 

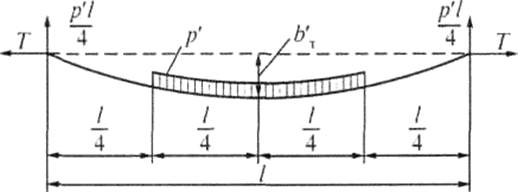
Рис. 11.9. Расчетная схема расположения нагрузок при ветровом расчете цепной подвески

 

                                              (11.22)

 

                                              (11.23)

 

Направление нагрузки р_э принято здесь таким же, как это пока­зано рис. 11.8 для р'. В тех случаях, когда несущий трос получает большие смещения, чем контактный провод, нагрузка р_э будет иметь отрицательное значение.

Величина полного ветрового отклонения несущего троса в середи­не пролета (рис. 11.10) исчисляется как сумма горизонтальной стрелы провеса b_Т, полученной тросом под действием ветра, ветрового откло­нения подвесных гирлянд β и прогиба опор γ_т (на уровне крепления гирлянд) под действием ветровой нагрузки на провода и тросы.

Величина полного ветрового отклонения контактного прово­да рассчитывается как сумма горизонтальной стрелы провеса кон­тактного провода b_к и прогиба опоры γ_к на уровне контактного провода под действием ветровой нагрузки на провода и тросы.

Для схемы, представленной на рис. 11.10, можно написать

 

b^/_к + γ_к – b^/_т – β – γ_т =е.                                             (11.24)

 

Подставим в полученное уравнение вместо величин b^/_к, b^/_т и e их значения из выражений (11.23), (11.22), (11.17) и заменим величину β ее зна­чением по формуле

 

                                               ,                                                           (11.25)

 

где λ — длина подвесной гирлянды; q_т — результирующая нагрузка несу­щего троса, определяемая по формуле

,

 

где g _T+ g_K — вертикальная нагрузка от веса проводов цепной под­вески.

 

 

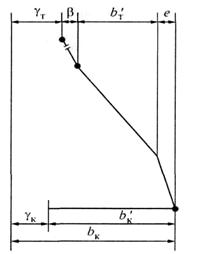
Рис. 11.10. Схема расположения проводов цепной подвески при отклонении ее ветром

 

При определении значений q_T и β по формуле (11.25) для уп­рощения расчета не учитываются изменения нагрузки вследствие перераспределения нагрузок между несущим тросом и контактным проводом. Как показали сравнительные расчеты, такое допуще­ние не отражается сколько-нибудь существенно на точности полу­чаемых результатов при определении значения р_э.

После подстановки в уравнение (11.24) указанных значений и замены р' в выражении (11.17) его значением из выражения (11.21) получим

 

 

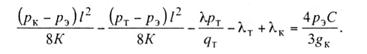
Умножив обе части уравнения на 8КТ/l² и перенеся члены, содержащие р_э в правую часть уравнения, получим

 

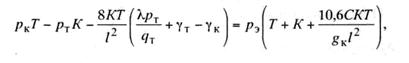
откуда

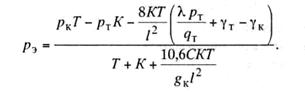                                (11.26)

После того как найдено значение р_э легко может быть определе­на величина полного ветрового отклонения контактного провода.

При вертикальной цепной подвеске с расположением контактного провода по оси пути наибольшее отклонение провода в середине пролета определяется по формуле

 

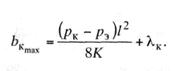
При расположении контактной подвески с зигзагом а (на прямом участке) наибольшее отклонение контактного провода от оси пути определяется по формуле

                                                                    (11.27)

Это отклонение имеет место в точке, отстоящей от середины пролета на расстоянии

 

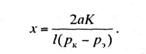
Величину наибольшего допускаемого пролета можно получить из формулы

 

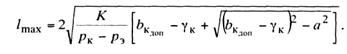                    (11.28)

 

Соответствующие формулы для кривых участков получат вид:

 

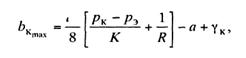                                                                       (11.29)

                           (11.30)

 

При желании учесть в расчете лишь часть действующих факторов и пренебречь влиянием остальных соответствующие формулы для оп­ределения значений р_э и b_к легко могут быть получены из выражений (11.26) и (11.27), если принять в них величины γ_к, λ, а равными нулю.

Так как в выражение (11.27) для определения значения р_э входит величина l, при решении уравнений (11.28) и (11.30) приходится при­бегать к методу последовательных приближений. Для этого, задав­шись значением l, найденным, например, по формулам (11.28) или (11.30) для случая, когда р_э = 0, определяют для этого значения l вели­чину р_э по формуле (11.26). Подставив найденную величину р_э в вы­ражение (11.28) или (11.30), находят новые значения l, для которых вновь могут быть определены соответствующие им значения р_э.

Можно также, задаваясь величиной l и определяя соответству­ющие значения р_э, находить по формулам (11.27) и (11.29) значе­ния b_Кдоп, которые должны получаться равными 0,5 м или незна­чительно отличаться в меньшую сторону.

Значение натяжения несущего троса Т в выражении (11.26) следует брать при температуре и нагрузке для режима наибольшей ветровой нагрузки.

Если определение допустимых длин пролетов производится до выпол­нения механических расчетов цепной подвески, величину Т в выражении (11.26) можно принимать равной 0,65 Т_mах для медного несущего троса и 0,75 Т_mах — для стального или биметаллического (сталемедного).

Величину Т_о, входящую в формулу (11.19) для определения сред­ней длины струны, принимают при медном несущем тросе равной 0,75 Т_mах, при стальном или биметаллическом (сталемедном) 0,8 Т_mах.

Зигзаг контактных проводов на прямых участках принимается рав­ным ± 0,3 м, наибольший вынос у опор на кривых участках 0,4 м.

Длину подвесной гирлянды К можно принимать для контактной подвески постоянного тока равной 0,5 м при двух изоляторах в гир­лянде, а для переменного тока 0,7 м при трех изоляторах в гирлянде и 0,85 м при четырех. В случае применения малогабаритных подвесных изоляторов эти данные соответственно уменьшаются.

Величины дополнительного прогиба опор под действием вет­ровой нагрузки γ_т и γ_к должны определяться с учетом давления ветра как на провода цепной подвески, так и на усиливающие и другие провода, подвешенные на данных опорах.

При наличии только проводов контактной цепной подвески величи­ны γ_к и γ_т, для однопутных консольных современных железобетон­ных опор можно принимать для скорости ветра 30 м/сек равными γ_к =0,015 и γ_т = 0,022 м.