ГЛАВА 9

РАСЧЕТЫ УСИЛИЙ В ОПОРАХ

ПРИ ОБРЫВЕ ПРОВОДОВ

 

Статистика повреждений контактной сети показывает, что обрыв проводов контактной сети занимает в ней заметное место, каждый раз приводя к большим сбоям в графике движения поездов. Для того чтобы последствия при этом были как можно меньшими, необходимо, чтобы обрыв проводов не приводил к разрушению поддерживающих и опорных конструкций. А для этого следует режим обрыва проводов рассматривать как один из расчетных (особых) режимов выборе параметров поддерживающих опорных конструкций. Поэтому необходимо рассмотреть процессы, возникающие при обрыве проводов, а также усилия, передающиеся на опорные конструкции. Как показывает статистика, случаев одновременного обрыва двух или более проводов контактной сети не более 5%. Причем такие ситуации возникают обычно при повреждении и поломке опоры от других причин. Поэтому в расчетах предусматривается обрыв одного из проводов контактной сети. Наибольшее место в статистическом ряду занимают обрывы несущего троса или контактного провода, их обрыв приводит к наиболее тяжелым последствиям, хотя на опорах контактной сети располагается ряд линий различного назначения.

Обрывы несущего троса вызываются в основном их механическими повреждениями и пережогом в месте короткого замыкания: при пробое изоляторов, при задевании случайно выходящими за габариты подвижного состава грузами или поврежденными частями ЭПС и др. Эти же причины могут вызвать и обрывы контактных провод, однако чаще всего контактный провод обрывается из-за пережога.

Обрыв провода представляет собой сложный динамический процесс, развивающийся во времени, начинаясь от одного установившегося состояния при неповрежденной подвеске и заканчиваясь другим, также установившимся состоянием уже поврежденной подвески (хотя и продолжающийся доли секунды). Сложность процесса и большое число влияющих факторов и определили то, что рекомендации для расчетов основываются на экспериментальных данных.

В большой мере влияние обрыва проводов на несущие конструкции зависит от возможности продольного перемещения точек подвеса провода вдоль пути при обрыве проводов. В этом смысле условия получаются различными для подвесок на консолях опор, на гибких и жестких поперечинах.

При обрыве провода силы его натяжения по обе стороны от точки подвеса становятся разными. В точке подвеса несущий трос уложен с некоторым перегибом в специальное седло и, кроме того, зажимается в седле специальной плашкой, что препятствует его продольному перемещению относительно седла. Однако при возрастании упомянутой разности натяжений до определенного значения трос проскальзывает в седле. При этом разность натяжений падает и проскальзывание прекращается. Кроме того, изоляторное звено само поворачивается в сторону от обрыва, что дает тот же эффект, что и проскальзывание. На консольных опорах также поворачиваются консоли, а на гибких поперечинах отклоняются поперечные тросы, чего нет на жестких поперечинах. Контактные провода подвешены на достаточно длинных струнах и их перемещение менее стеснено, чем несущих тросов.

Рассмотрим влияние проскальзывания провода относительно точки подвеса, а также влияние продольного смещения самой точки подвеса (например, при отклонении изоляторного звена или при повороте кон соли) на натяжение провода подвески, состоящей из одного пролета.

В обоих вариантах (рис. 9.1, а и б) провод подвешен в точках А и В при расстоянии между ними (пролете), равном l, м, и натяжении Н₁. В первом случае вследствие проскальзывания провода на длину у его длина увеличилась и, следовательно,

натяжение упало до значения Н₂. Длина пролета l сохранилась. Во втором случае за счет смещения точки подвеса при перекосе изоляторного звена или повороте консоли опора В сместилась. Длина пролета уменьшилась до l₂, а натяжение упало до Н₂^/ . На практике можно принимать Н₂^/ = Н₂, т.е. проскальзывание провода в зажиме (седле) или отклонение точки подвеса на одно и то же значение дает одинаковое изменение натяжения в проводе.

 

 

Рис. 9.1. Изменение натяжения в проводе при проскальзывании и уменьшении длины пролёта

 

По выражениям (3.22) и (3.23) (при L= L_п, l =l₁, q =g, H=H₁ и f=f₁) длина провода L₁

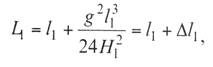                                        (9.1)

или

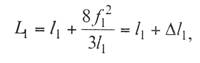                                        (9.2)

где Δl₁ – превышение длины провода по сравнению с длиной пролета;

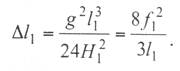                                          (9.3)

Значение Δl₁ при применяемых натяжениях и стрелах провеса составляет ничтожную долю относительно длины пролета l₁.

Рассмотрим, как влияет проскальзывание провода через седло в точке подвеса (см. рис. 9.1, а). Сначала определим начальную (без натяжения) длину провода l₀ в пролете. Для этого из длины L₁ в выражении (9.1) вычтем упругое удлинение:

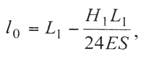
где Е и S – соответственно модуль упругости материала провода и площадь поперечного сечения.

Во втором члене этого выражения заменим L₁ на l₁, т.е. опустим малую величину второго порядка. Подставим значение L₁ из выражения (9. 1), тогда

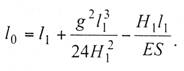                                             (9.4)

Если провод проскользнул в седле на γ_м, то его начальная длина теперь будет  l₀+γ . При этом натяжение уменьшится до Н₂. Тогда

                                        (9.5)

Сравним выражения (9.4) и (9.5). Отсюда

                                 (9.6)

В выражении (9.6) заменим Н₂ на kН₁ (коэффициент k покажет, какую часть Н₂ составит от Н_j):

                                     (9.7)

Задавшись значением k, получим соответствующее значение γ.

Расчет примера показывает, что при меньшей длине пролета и при большем натяжении получается меньшее проскальзывание.

Если рассматривать линию с несколькими равными по длине пролетами, то проскальзывание в точках подвеса убывает по мере удаления от места обрыва. Под γ в этом случае надо понимать разность проскальзывания у опор, ограничивающих рассматриваемый пролет. Опыт показывает (см. рис. 9.5), что такие проскальзывания, как и разность проскальзываний, превышают значения, приведенные в примере.

Во втором случае (см. рис. 9.1, 6), т. е. когда после обрыва точка В сместилась влево на значение γ (за счет отклонения изоляторного звена или поворота консоли), а проскальзывания не было, выражение (9.5) заменяется выражением

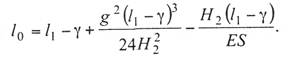                                 (9.8)

Соответственно вместо выражения (9.7) будем иметь:

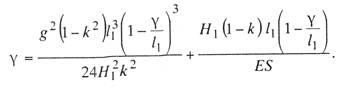                           (9.9)

Так как γ<<l₁, то на точность расчета практически не повлияет, если мы примем γ / l₁ = 0, и тогда выражения (9.7) и (9.9) будут одинаковыми. Отсюда можно сделать вывод, что проскальзывание провода на длину γ или отклонение точки подвеса на такое же значение практически приводит к одинаковому снижению натяжения.

Рассмотрим, как протекает процесс перемещения контактного провода цепной подвески при его обрыве в какой-то точке анкерного участка. Начнем с некомпенсированной подвески. С одной стороны провод жестко (неподвижно) закреплен на анкерной опоре, а с другой стороны — с помощью средней анкеровки. Незначительным ее перемещением при обрыве провода будем пренебрегать. Пусть после обрыва провода слева от него останется n₁ неповрежденных пролетов общей длиной L₁, а справа от него – n₂ пролетов общей длиной L₂ (рис. 9.2). Все точки провода у опор А_1, А₂, ..., А_n1 сместятся влево за счет уменьшения натяжения провода. Оно, собственно, не упадет до нуля только вследствие появления в натяжении струн при их перекосе горизонтальной (вдоль провода) составляющей. Аналогичное положение будет и в правой части анкерного участка на длине L₂. Наибольшее перемещение получат точки А_n1 и В_n2 провода, расположенные ближе к месту обрыва. По мере удаления от места обрыва эти перемещения уменьшаются.

Так как стрелы провеса провода между струнами очень незначительны, то для получения общего представления о характере явления заменим провод упругим растянутым стержнем (рис. 9.3). Процесс исчезновения растягивающей силы Н₀ можно представить себе как приложение в точке обрыва новой силы Н₁, равной по величине силе Н₀, но противоположной ей по направлению. В итоге в точке А_n1 растягивающая сила обратится в нуль. Исходя из принципа независимости действия сил, можно считать, что на упругие удлинения, вызванные силой Н₀, наложатся упругие сокращения, вызванные силой Н₁. Стержень переходит от состояния растяжения силой Н₀ к нейтральному состоянию (при Н₁ = Н₀) не мгновенно. Переход представляет собой процесс, развивающийся во времени. Мгновенное изменение натяжения по всей длине провода от Н₀ до нуля было бы возможным только при массе стержня, равной нулю.

 

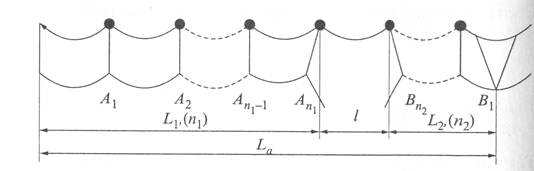
Рис. 9.2. Схема пояснения процессов, происходящих при обрыве контактного провода

 

Рис. 9.3. Растянутый стержень

 

Если представить себе, что упругий стержень состоит как бы из нескольких последовательно соединенных стержней с массой m₁, m₂, …, m_n1, то приложение силы Н₁ вызвало бы смещение всех точек А₁, ..., А_n1, убывающее от А_n1 к точке О. Соответственно различными получатся ускорения этих точек при их смещении влево, а следовательно, и разная реакция масс m₁, m₂, …, m_n1, т.е. убывание силы от значения Н₀ на длине от А_n1 до нуля будет неодинаковым, и наибольшим это убывание будет в точке А_n1. Вместе с тем по истечении небольшого промежутка времени (времени перехода от одного устойчивого состояния к другому) натяжение Н по всей длине стержня упадет до нуля. Следовательно, при обрыве провода сила Н изменяется неодинаково по всей длине стержня, а распространяется волной от точки А_n1 к точке О. Поскольку в этом процессе участвуют силы инерции масс, то возникают затухающие продольные колебания сложного характера. Здесь важно то, что в этом процессе силы, действующие на поддерживающие конструкции (при контактном проводе это струны), получают значения большие, чем по окончании переходного процесса.

Аналогично протекает процесс обрыва и компенсированного провода с той лишь разницей, что в нем участвует и масса компенсирующего груза. В какой-то момент времени в процессе обрыва провода натяжение струн достигает значения, при котором наиболее короткие струны (в середине пролета) срываются с контактного провода, что и было отмечено в специально поставленном эксперименте.

Обрыв провода увеличивает натяжение несущего троса за счет наклона струн и перекоса фиксаторов (см. гл. 3). При установившемся режиме сумма этих дополнительных натяжений троса уравновешивает силу тяжести компенсирующего груза, если в результате обрыва провода он не опустился на землю. В последнем случае уравновешивает остаточное в месте анкеровки натяжение в контактном проводе, оборванный же провод провисает до земли.

Проведенными опытами показано, что поддерживающие и опорные конструкции получают значительно большие нагрузки при обрыве несущего троса.

Рассмотрим установившееся положение подвески после обрыва троса на одном анкерном участке (рис. 9.4), полученное при проведении упомянутого ранее эксперимента в режиме без добавочных (имитирующих гололедные) нагрузок.

Анкерный участок полукомпенсированной подвески марки ПБСМ-95 + 2МФ-100 состоит из 17 пролетов, каждый длиной 75 м. В десятом пролете расположена средняя анкеровка. Обрыв произошел (был сымитирован) в четвертом пролете между опорами З и 4. Начальное натяжение в несущем тросе 21 кН, а установившееся после обрыва у анкерной опоры в разных опытах от 9 до 11 кН. Оборванные концы несущего троса опустились на землю. На опорах 3 и 2 консоли повернулись в сторону от точки обрыва соответственно на 45 и 10⁰ и вправо от обрыва на 55, 10 и 7°. При обрыве трос, закрепленный в седле с плашками (см. рис. 13.7), переместился в сторону от обрыва: влево на опорах 3, 2 и 1 (см. рис. 9.5) соответственно на длину 1,05; 0,75 и 0,30 м; справа на опорах 4, 5 и 6 соответственно на длину 1,3; 0,85 и 0,72

 

 

 

 

 

 

 

Рис. 9.4. Обрыв несущего троса в эксперименте

 

м. При проведении опытов было измерено, что продольные силы реакции, противодействующие проскальзыванию троса, равны примерно 3,0—3,5 кН при закреплении троса в седле с помощью плашки и 1,5—1,75 кН для незакрепленного троса. В пролетах 7÷10 перемещения малы.

Вследствие смещения частей несущего троса влево и вправо от точки обрыва струны левой и правой частей получат наклоны в противоположные стороны. Средние струны в «пролете обрыва» оборвались.

В смежных пролетах струны сохранились, но часть из них ослабла, и контактный провод повис как свободно подвешенный, т.е. его стрела провеса определялась силой тяжести и его натяжением.

Расположение проводов в пролетах слева и справа от обрыва различно. До обрыва длина несущего троса в каждом пролете была больше длины пролета на Δl [см. выражения (9.1) и (9.2)]. Общее удлинение несущего троса от анкерной опоры до средней анкеровки (от первого до середины десятого пролета) 9,5 Δl. Слева до середины четвертого пролета упругое удлинение троса З,5 Δl, а справа 6,0 Δl. После обрыва трос как растянутая пружина будет стремиться сократить свою длину, при этом справа на большую длину, чем слева. В результате этого сокращения консоль у смежной правой опоры 4 повернется на 55°, а у левой опоры 3 – на 45° и в другую сторону. Положение элементов контактной сети после обрыва троса в системах с поворотными и полузащемленными консолями примерно одинаковое. Гирлянды подвесных изолятор сохранят почти везде вертикальное положение, что говорит о небольшой разнице в натяжении троса по обе стороны от точки его подвеса. Эта разница в натяжениях уравновешивается силой трения троса в седле, не допускающей дальнейшего его проскальзывания, и силой трения в шарнирах консоли, препятствующей дальнейшему ее повороту относительно опоры. Разность этих сил не велика, и это видно из того, что консоли под их действием поворачивались не полностью, и не только разность сил, но и сами силы получают небольшие значения.

Это объясняется тем, что очень незначительное увеличение длины провода, подвешенного с малой стрелой провеса, приводит к резко снижению его натяжения. Это может произойти в неизменном по длине пролете вследствие проскальзывания провода в точке подвеса или при уменьшении длины пролета за счет отклонения изоляторов поворота консоли, или от того и другого вместе.

В результате этих продольных перемещений несущего троса при его обрыве натяжение в нем растет по мере удаления от места обрыва у каждой опоры и над каждой струной. Проведенные эксперименты показали, что продольная нагрузка на опоры при установившемся режиме после обрыва оказалась незначительной. Однако записи усилий в переходном режиме, выполненные с помощью осциллографа, показали, что именно в этом режиме возникают максимальные нагрузки на консоли и опоры. После обрыва троса ближайшие к месту обрыва струны так перекашиваются, что почти продолжают линию троса, передавая остающееся в нем натяжение на контактный провод. При этом контактный провод в месте разрыва троса получает повышенное натяжение. Под влиянием возникшего натяжения наиболее короткие, т.е. наиболее перекошенные струны рвутся.

В описываемых исследованиях испытывали подвеску с рессорным тросом. В момент после обрыва несущего троса изоляторное звено получило некоторый наклон (рис. 9.5), консоль же, обладающая большей массой, почти не сдвинулась с места. Горизонтальная составляющая натяжения троса Т₂ (слева) стала больше, чем горизонтальная составляющая Т₁ (справа). При этом рессорный трос СDЕF занял положение, показанное на рисунке. Элемент рессорного троса ЕF ослабился, а элементы СD и DE натянулись, передавая большую часть натяжения несущего троса в элементе RС через подрессорные струны DМ и ЕN на контактный провод К. Опыты проводили на подвеске с нескользящими подрессорными струнами.

 

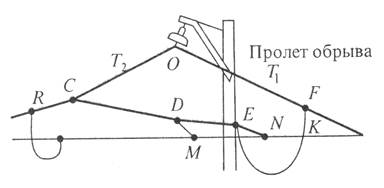
Рис. 9.5. Расположение проводов подвески у опоры в пролете обрыва

Горизонтальная составляющая натяжения Т₂ будет уравновешиваться горизонтальной составляющей остаточного натяжения Т₁ и силой инерции масс консоли и изоляторного звена. Вертикальные составляющие усилий Т₂ и Т₁ передадутся на консоль, вызвав дополнительное сжатие ее стрелы (кронштейна) и растяжение тяги. С поворотом консоли сначала упадет натяжение Т₂, а затем вертикальная нагрузка на точку О. При установившемся режиме она будет иметь небольшое значение. При скользящих подрессорных струнах остаточное натяжение в несущем тросе будет передаваться на контактный провод за счет перекоса пролетных струн, и можно думать, что вертикальная нагрузка на консоль и опору в переходном процессе будет ниже.

Расчет консоли и опоры на динамическое воздействие сил при обрыве несущего троса сложен, и поэтому его заменяют статическим расчетом, но с увеличенной нагрузкой. В данном случае для получения расчетной динамической нагрузки предлагается нагрузку Q от силы тяжести проводов подвески умножить на динамический коэффициент k_д, т.е.

                                              (9.10)

Нагрузку Q принимают для наиболее тяжелого, гололедного режима. Толщину стенки гололеда на проводах рекомендуют принимать равной 0,5 расчетной, а динамический коэффициент k_д =1,9. В этом случае получается вывод, сходный с ситуацией в системах, рассматриваемых в сопротивлении материалов, при внезапном действии нагрузки, когда возникающие напряжения вдвое больше, чем при ее статическом действии.

При опорах с жесткой поперечиной условия по сравнению с подвеской на консольных опорах существенно изменяются, так как из продольного смещения точки подвеса исчезает поворот консоли. Однако в начальный момент, когда консоль еще не успела повернуться, складываются сходные условия. При установившемся режиме после обрыва несущего троса на жесткую поперечину будет действовать продольная (вдоль пути) сила, Р_ож, кН,

                                            (9.11)

где Q — сила тяжести подвески, кH; ψ₁ – коэффициент сопротивления перемещению троса в седле; Р_в — сопротивление выдергиванию зажатого троса, кН.

Для применяемых конструкций седла (см. рис. 13.7) сопротивление Р_в рекомендуется принимать равным 1,5 кН при тросе ПБСМ-95 и проводе М-120; 2,10 кН — для стальных тросов; 2,90 кН — для сталеалюминиевых тросов АС-185.

Коэффициент ψ₁ рекомендуется принимать равным 0,75 для троса ПБСМ-95; 0,7 — для троса М-120; 0,5 — для сталеалюминиевого троса АС-185; 0,2 — для стального троса С-70.

По результатам эксперимента сделан вывод, что максимальная вертикальная нагрузка Q_g [см. выражение (9.11)] по времени не совпадает с продольной нагрузкой в момент проскальзывания троса в седле. Поэтому при расчете жесткой поперечины на продольную (вдоль пути) нагрузку динамический коэффициент не вводят.

Необходимо отметить, что при проверке несущей способности опор эксплуатационным персоналом нужно пользоваться упрощенной методикой расчета Всероссийского научно-исследовательского института транспортного строительства (ЦНИИС) и ВНИИЖТ.

При проектировании контактной сети на кривых участках пути, а также при замене опор на действующих участках необходимо так же выполнять расчет опор на особую нагрузку от падения соседней опоры. При этом учитываются параметры не только контактной подвески, но и нагрузки от других проводов, подвешенных на опоре, а также давление ветра.