4.6. Основания и поддерживающие элементы опор

 

Фундаменты служат для закрепления опор в грунте и должны обес­печивать их устойчивое положение при любых неблагоприятных соче­таниях нагрузок. Классификация фундаментов (рис. 4.18) опреде­ляется схемой прилагаемых к ним сил (одиночные и групповые), способом установки (закапываемые, заливаемые, забиваемые), формой сечения (прямоугольные, круглые, двутавровые, трехлу­чевые), способом скрепления с опорой (заливаемые, болтовые, ста­канные, надеваемые на сваю, устанавливаемые в короб), конструк­цией (призматические, конические, свайные с ростверком).

При применении одиночных фундаментов (рис. 4.19) момент внешних (выворачивающих сил) уравновешивается моменте!.: ре­активных сил в грунте. Фундаменты опор с конструкциями, на­пример, с оттяжками (рис. 4.20, а, б), препятствующими выдерги­ванию или погружению опор в грунт, называют раздельными. Стрелки М на рис. 4.19 и 4.20 показывают направление момента М, действующего на фундамент, а стрелки в грунте — примерный характер реакций, вызываемых в нем.

При электрификации железных дорог около 70 % опор закреп­ляют непосредственно в грунте (нераздельные опоры) и примерно 30 % устанавливают в стаканные фундаменты (раздельные). Уста­новленная в стакан опора закрепляется омоноличиванием полос­ти между внутренними стенками стакана и наружной поверхнос­тью опоры цементным раствором. Широкое применение нашли клиновидные фундаменты конструкции В.И. Подольского для раздельного крепления опор контактной сети системы КС-200 и др. (рис. 4.20, в). Для закрепления в грунте раздельных центрифугированных железобетонных опор (типа С и СО) и стоек жестких попе­речин взамен ранее использовавшихся стаканных фундаментов и анкеров двутаврового сечения широко применяют трехлучевые же­лезобетонные фундаменты стаканного типа, а для крепления от­тяжек — трехлучевые анкеры, позволяющие уменьшить высокое сопротивление грунта при их вибропогружении.

Обозначают фундаменты буквами и цифрами: Т — трехлуче­вой, С — стаканного типа, А — анкер; первое число в обозначе­нии — несущая способность фундамента, тс м, второе число — длина фундамента, м, например, ТС-6,0-3,5.

Оттяжки изготавливают из круглой стали диаметром 16 мм и ис­пользуют для увеличения несущей способности опор. Обычно к верх­ней части опор крепят хомутами две оттяжки (на уровне несущего троса и контактных проводов), сходящиеся внизу на проушине анке­ра. Оттяжки могут быть неизолированными и изолированными. Последние применяют для предотвращения стекания через оттяжку блуж­дающих токов в случае высокой электропроводности грунта.

Подкосы применяют как элемент увеличения несущей способ­ности опор при невозможности использования оттяжек. Выполня­ют подкосы в виде протяженной, работающей на сжатие фермы, например решетчатой, уголковой (рис. 4.20, в). Нижним концом ферма опирается на анкер.

 

Рис. 4.18. Классификация фундаментов опор контактных сетей

 

Анкеры предназначены для крепления оттяжек или подкосов и клас­сифицируются по форме сечения: призматические, двутавровые, трехлучевые. Обозначение последнего — ТА.

Лежни и опорные плиты применяют для улучшения закрепления без фундаментных опор в грунте. Их изготавливают трех типоразмеров и обозначают: лежни—Л-1, Л-П, Л-Ш, а опорные плиты — ОП-1, ОП-П и ОП-1П. Первые две плиты выполняются в виде кругов, третья — прямоугольной формы (600 х 800 мм, толщиной 50 мм).

Все фундаменты, анкеры, лежни и опорные плиты изготавлива­ют из ненапряженного железобетона.

Для закрепления железобетонных опор в районах вечной мерз­лоты и глубокого сезонного промерзания грунта применяют спе­циальные конструкции: сваи длиной 8 и 10 м; анкеры стоечного типа Длиной 4,5 м с опорной плитой в основании; свайные забиваемые анкеры длиной 10 м, а также теплоизоляцию фундаментной части, препятствующую оттаиванию грунта. Для закрепления в грунте металлических опор гибких поперечин применяют железобетонные свайные, а также раздельные (рис. 4.20, г) фундаменты, состоящие из двух блоков с анкерными болтами для крепления.

 

 

                                        

 

Рис. 4.19. Схемы закрепления опор на выворачиваемых фундаментах: бесфун­даментное крепление (а); с лежнями (б); призматическое (в); ступенчатое (г); двутавровое (д)

 

Обозначают блочные фундаменты буквами и цифрами: Р — раздельный, Ф — фундамент, первая цифра — тип блока по опалубочным размерам, вторая — тип армирования. Перспективные фундаменты опор гибких поперечин (рис. 4.20, д) состоят из железобетонной плиты -ростверка, сквозь отверстия в которой забивают сваи. Сваи и ростверк соединяют между собой сваркой с помощью специальных металли­ческих анкеров, заделанных в бетон, и съемных накладок, а затем омоноличивают бетонными оголовками. Для облегчения конструк­ции ростверка в нем устраиваются «окна», заполняемые грунтом.

 

Рис. 4.20. Схемы закрепления опор на различных выдергиваемых фундаментах: с анкером и подопорной плитой (а); ступенчатый фундамент с анкером (б, в): раздельный (г); свайный с ростверком (д); 1 — анкер: 2 — подопорная плита; 3 — опора; 4 — оттяжка; 5 — ступени; б — подкос: 7 — свая; 8 — ростверк; 9 — раздельные фундаменты

 

 

4.7. Расчет закрепления опорных конструкций в грунте

 

Нагрузки, приложенные к опоре, передаются на грунт. При этом они не должны приводить к его разрушению, так как опора может потерять устойчивость и эксплуатация линий, расположенных на этих опорах, станет невозможной. Конструкции закрепления опор зави­сят от вида и значения нагрузок, качества грунта, профиля местности и т. д. Методы расчета закрепления опор будут рассмотрены ниже.

Характеристики грунта и расчетные эпюры давлений. «Пассив­ное давление грунта» — термин, в котором грунт рассматривают как сыпучее тело, т.е. совокупность мелких твердых однородных час­тиц, не имеющих связи друг с другом (лишенных силы сцепления). Основными характеристиками грунта в этом случае являются угол естественного откоса  и угол внутреннего трения .Силу тяжести G отсеченной части объема сыпучего тела (рис. 4.21, а) можно разложить на две составляющие  N и Т. Сила N уравновеши­вается нормальной реакцией остальной части грунта, а сила Т — силой трения в плоскости С—С. При некотором (предельном) угле наклона плоскости С—С сила трения окажется недостаточной и грунт начнет сползать вниз. Это может случиться, если (здесь  равен коэффициенту трения f или тангенсу угла трения между частицами тела;  — угол наклона плоскости С—С к горизонту). Частицы грунта будут сползать до тех пор, пока не установится рав­новесие между составляющей силой тяжести и силой трения. Угол наклона плоскости С—С, соответствующий такому положению, на­зывают углом естественного откоса сыпучего тела  (рис. 4.21, б).

При изучении вопросов, связанных с условиями равновесия не­которого объема грунта, приходится учитывать силы трения од­ной части грунта о другую. Коэффициент трения в этом случае для внутренних слоев будет больше, чем для верхних слоев. Однако в расчетах принимают .

Для определения наибольшего допустимого нажатия на грунт рассматривают подпорную стенку А В (рис. 4.21, в) и предполагают, что выше точки А грунт имеется только справа и ограничивается плоскостью ЕС. Стенка удерживает в равновесии некоторый объем грунта, который стремится сползти в ее сторону. Если давление со­здается стенкой (например, сила Р стремится переместить стенку параллельно самой себе вправо), то в грунте будет развиваться ре, активная сила, и при увеличении силы Р наступит момент, когда стен­ка придет в движение, а часть грунта будет выпираться стенкой вверх и вправо по линии А С (плоскость выпирания). Силу, вызывающую такое выпирание, называют пассивной силой, а давление — пассив­ным давлением _пасс (штриховая линия).

Рис. 4.21. Расчетные схемы определения пассивного давления грунта.

 

Рассмотрим эпюру напряжений в грунте у передней и задней сте­нок фундамента. Подобно другим телам грунт в известных преде­лах нагрузки обладает упругостью, т.е. между напряжением о', на глубине у и деформацией , вызванной этим напряжением, су­ществует зависимость:

                                                                                                                            (4.22)

Коэффициент С_у зависит от уплотненности грунта. Обычно прини­мают, что он пропорционален глубине. Если обозначить через С_h ко­эффициент для глубины h, то коэффициент для глубины у равен

                                           С_у=С_hу/h.                                                              (4.23)

Как только внешние силы повернут фундамент на некоторый угол а относительно точки, лежащей на глубине у₀ (рис. 4.22, а), в грунте возникнут реактивные давления, которые уравновесят оп­рокидывающий момент и внешние силы. При этом центр враще­ния фундамента должен лежать на глубине, меньшей глубины его заложения. Если бы центр вращения лежал ниже основания фун­дамента, то, очевидно, фундамент смещался бы в одну сторону.

 

Рис. 4.22. Расчетная схема для определения эпюры напряжений в грунте

 

Следовательно, в грунте не могли бы развиваться реакции различ­ного знака, которые необходимы для создания пары сил, уравно­вешивающей опрокидывающий момент. Для определении закона распределения усилий в грунте возле фундамента исходят из пред­положения абсолютной жесткости фундамента или заложенной в грунт части опоры. Тогда

                                                                                               (4.24)

Подставим в выражение (4.22) значения С_у и _у  из выражений (4.23) и (4.24)

 

                                                                               (4.25)

 

Если у = h, то '_y ='_h=C_h(y₀-h)tg.

Подставив из последнего выражения значение С_htg в уравне­ние (4.25), получим

                                                                                                (4.26)

 

Таким образом, напряжение в грунте изменяется по высоте фун­дамента по закону параболы. Уравнение (4.25) показывает, что при у = y₀,, положительно, при у =y₀ равно нулю и при у >y_о отрица­тельно (рис. 4.22, б).

Большинство применяющихся методов расчета фундаментов основывается на рассмотренной эпюре напряжений в грунте. В неко­торых методах исходят из условия, что (рис. 4.22, в), т.е. наибольшее напряжение в грунте (у нижней точки фундамента) при­равнивают к пассивному давлению в этой точке и получают напря­жения в верхней части эпюры, выходящие за линию пассивных давле­ний (заштрихованная площадь). Методы расчета, основанные на ис­пользовании таких эпюр, не дают представления о запасе устойчиво­сти опоры и, естественно, не могут указать, допустимо ли достижение напряжений в грунте, равных пассивным давлениям, и если допусти­мо, то на какой части фундамента. Поэтому единственно правиль­ным является расчет по предельному состоянию фундамента.

Предельное сопротивление грунта. Многочисленные эксперименты показали, что потеря фундаментом устойчивости не сопровождается опи­санным ранее выпиранием призмы грунта. Следовательно, предельное сопротивление грунта наступает раньше, чем начнется выпирание грун­та. Деформация грунта зависит не только от нагрузки, но и изменяется во времени. При этом в каждом случае имеется некоторая статическая сила р_пр характеризующая предел устойчивости. При действии на опо­ру сил, меньших этого значения (Р < Р_пр) деформации грунта, а следова­тельно, и перемещения 6 фундамента с течением времени затухают и за­тем остаются постоянными (рис. 4.23, а). Если же Р > Р_пр , то дефор­мация грунта и перемещения фундамента не затухают и продолжают увеличиваться, пока действует нагрузка. Скорость v этих перемещений после приложения нагрузки быстро уменьшается и в течение некоторого времени практически постоянна, но будет тем больше, чем больше при­ложенная к опоре нагрузка Р (рис. 4.23, б). В конце процесса роста деформаций скорость резко увеличивается и фундамент «опрокидывается». В зависи­мости от нагрузки время до этого момента может изме­ряться от нескольких десят­ков лет (при нагрузках, не­значительно превышающих Р_п ) до нескольких дней, ча­сов и даже минут (значитель­но превышающих Р_пр).

 

       

 

Рис. 4.23. Перемещение (а) и скорость пе­ремещения v (б) фундамента в зависимости от времени для различных значений силы P

 

При расчете поворота фундамента учитывают действие постоянных на­грузок и изменение направ­лений временной (ветро­вой) нагрузки. Кратковре­менные нагрузки, даже зна­чительно превышающие расчетные предельные, не вызывают существенных перемещений и не являются опасными. Не представляют опасности и гололедные нагрузки, так как они обычно действуют в условиях промерзшего грунта, что зна­чительно увеличивает предельный момент.

В рассматриваемом методе расчета предельное давление, ока­зываемое вертикальной стенкой грунта на фундамент, определя­ется по формулам

                                 

    при   b0.3 м                                     (4.27)

и

                                     при b<0,3 м ,                                 (4.28)

где k — коэффициент возможных отклонений грунта от норматив­ных; т — допускаемое напряжение грунта на глубине 1 м; с — тол­щина и b — ширина фундамента.

Значение  пропорционально глубине у и зависит от ширины фун­дамента b. При бесконечно длинной стене, т.е. в условиях плоской задачи, когда взаимодействие разрушаемой и неразрушаемой части грунта отсутствует, коэффициент 1+с/b обращается в единицу. Следовательно, в условиях плоской задачи коэффициент m₀ можно рассматривать как характеристику грунта, равную предельному на­пряжению  на глубине у= 1. Коэффициент с зависит от рода и со­стояния грунта. Коэффициент однородности k учитывающий возмож­ное отличие фактических характеристик грунта от их нормативных значений, принимают равным 0,7. В таблице приведены нормативные значения m₀ и с, а также предельное давление _п фундамента на грунт.

Рассмотрим эпюру напряжений в грунте по передней и задней стен­кам фундамента в предельном состоянии. Если нагрузка, вызвавшая давление (см. рис. 4.22,5), продолжает увеличиваться, то эпюра снача­ла примет вид, представленный на рис. 4.24, а и затем на рис. 4.24, 6. Отличие этой эпюры от более удобной для расчета   (рис. 4.24, в) невели­ко и объясняется тем, что реактивный момент увеличивается незначи­тельно (заштрихованная часть на рис. 4.24, б). В этом случае наиболь­ший реактивный момент определяется как сумма моментов грузовых площадей F₁ и F₂, умноженных на расстояния от их центров тяжести до центра вращения О. Глубина центра вращения д'₀ определяется из усло­вия равенства нулю суммы всех горизонтальных сил: F₁ –F₂ - Р = 0. Временное сопротивление определяют по выражениям (4.27) и (4.28).

Таблица    

Характеристики грунтов

 

Рассмотрим эпюры напряжений в грунте у подошвы фундамен­та в предельном состоянии. Опрокидывающий момент M, вызы­вающий напряжения у подошвы фундамента, может быть создан как горизонтальной силой P, так и вертикальной силой N_p при ее эксцентричном положении относительно оси фундамента. В за­висимости от опрокидывающего момента эпюра напряжений у подошвы фундамента, уравновешивающая силу N (где N — рав­нодействующая сил реакции грунта) будет принимать тот или иной вид. Так, при наличии одной силы N_p   приложенной в цент­ре фундамента, напряжение грунта  и ему соответству­ет деформация ₀. Эпюры напряжений и деформации будут иметь вид прямоугольника (рис. 4.25, а). При появлении опрокидываю­щего момента М, вызванного эксцентричным приложением силы N_p или введением новой силы Р, фундамент получит некоторый на­клон. Эпюры напряжений и деформаций получат вид, приведенный

 

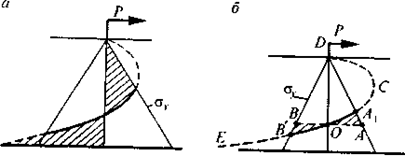
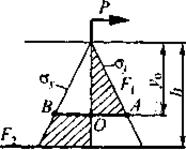
Рис. 4.24. Расчетная схема для выбора расчетной эпюры по передней и задней стенкам фундамента в предельном состоянии

 

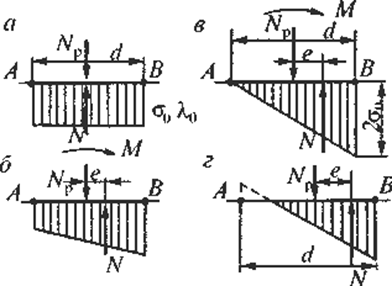
Рис. 4.25. Эпюры давлений у по­дошвы фундамента в пределах уп­ругого сжатия грунта

 

Эпюры напряжений и деформаций получат вид, приведенный на рис. 4.25, б где силы N_p и N создают пару, уравновешиваю­щую опрокидывающий момент М. Когда увеличивается момент М, возрастает наклон фунда­мента и, следовательно, должен увеличиться момент пары сил. Сила N_p (сумма всех вертикаль­ных сил, действующих на соору­жение, включая силу тяжести фундамента) может быть по­стоянной только при увеличе­нии плеча пары N и N_p , т.е. по­степенного удаления силы N от силы N_p и приближения ее к краю фундамента.

При дальнейшем увеличении опрокидывающего момента эпюра примет вид, представленный на рис. 4.25, г. Так как грунт не может работать на растяжение, то у точки А подошва отрывается от него и происходит так называемое «раскрытие шва». Реактивный момент бу­дет тем большим, чем на большей длине это произойдет. Площадь эпю­ры давлений все время остается постоянной, равной сумме вертикальных сил, а поэтому е увеличивается при возрастании напряжения под реб­ром Я При достижении определенного предела сжатия грунта оно уже не будет упругим и нарастание напряжения под ребром В (рис. 4.26, а) будет происходить медленнее, чем увеличение угла поворота (до этого предела указанные величины находятся в линейной зависимости). Точ­кой D отмечено значение, какого бы достигло напряжение, если бы грунт при всех значениях а отвечал закону упругости. Если после некоторого напряжения _п сопротивление грунта почти не увеличивается, то, оче­видно, эпюра получит вид, представленный на рис. 4.26, б. Без ощути­мой погрешности можно для определения предельного момента (в запас прочности) принять взамен эпюры на рис. 4.26, а фиктивную эпюру давлений, показанную на рис. 4.26, в, так как изменение эксцентриситета, очевидно, будет nнезначительным.

 

 

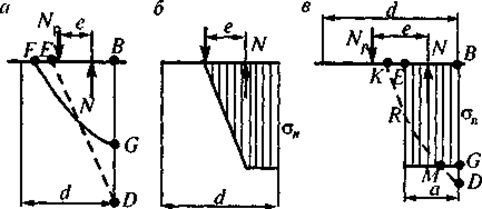
Рис. 4.26. Эпюры давлений у подошвы фундамента за пределами упругого сжатия грунта

 

Некоторое уменьшение эксцентриситета из-за потери площади МGD компенсируется увеличением его от потери площади КЕК. Эту эпюру, очевидно, и можно принять для расчета.

При использовании методов расчета, основанных на распре­делении усилий в грунте при эксплуатации, наибольшую труд­ность представляет разделение усилий между подошвой и стенка­ми фундамента. Обычно сначала определяют допустимый момент, действующий на подошву фундамента, а затем, взяв остаток меж­ду расчетным моментом и моментом, воспринимаемым подошвой, проверяют напряжение у боковых стенок; полагая тем самым, что деформации грунта у подошвы не связаны с деформациями грун­та у боковых стенок, что, конечно, неверно. Также неверным яв­ляется расчет, основанный на каком-либо другом распределении эпюр в состоянии устойчивости. Пока не имеется данных, кото­рые могли бы связать деформации грунта у подошвы и боковых стенок между собой.

Наиболее удобным, видимо, будет расчет без учета распреде­ления опрокидывающего момента между подошвой и боковыми стенками. Этого можно достигнуть, определяя наибольший оп­рокидывающий момент (предельный) как сумму наибольших мо­ментов для боковых стенок и подошвы. Такой подход будет верным, так как опора вывернется только после того, как момент внешних сил превысит этот суммарный наибольший момент сил реакций боковых стенок и подошвы.

При определении предельного опрокидывающего момента проверку на деформации (наклон фундамента) можно не проводить, так как характеристики грунта в нормативах заданы, исхо­дя из условий допустимости соответствующих перемещении фун­даментов опор при эксплуатации.

Предельный опрокидывающий момент для призматического фундамента. Расчетная эпюра активных и реактивных сил, дей­ствующих на фундамент в предельном состоянии, представлена на рис. 4.27. В предельном состоянии на фундамент действуют горизонтальная Р₀ и вертикальная (сила тяжести) N₀ силы.

Если на опору в одной вертикальной плоскости действует не­сколько горизонтальных сил Р₁ , Р₂,…, Р_п с плечами H₁,H₂,..,H_n и моментов M₁ , M₂, ..., M_n, то для расчета удобно найти суммарный момент относительно поверхности земли:

                                          M₀=                                                       (4.29)

Частное от деления M₀ на   равно эквивалентному плечу этой силы Н=М₀/Р₀.

Для определения суммар­ного реактивного момента составим два уравнения рав­новесия. Первое из них мо­жет быть представлено в виде

 

                                                                       (4.30)

где R₁ и R₂— равнодей­ствующие сил реакций грун­та на боковые стенки.

Второе условие равно­весия—сумма моментов от­носительно точки О:

                                 

Рис. 4.27. Расчетная схема нагрузки при­зматического фундамента в предельном состоянии

 

В этих уравнениях

; 

                                                                                 (4.31)

Соответственно

;

                                                               (4.32)

где my₀ и  mh — предельные давления на боковые стенки соответственно на глубине y₀ и h.                                                               

Значения величин из выражений (4.31) подставим в уравнение (4.30)

 

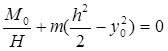                                (4.33)

 

Подставляя   выражения   (4.31)   в (4.32) и полученный результат в (4.7.9), получим

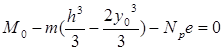                                                                 (4.34)

Из уравнения (4.33) можно определить

 

                                                                            (4.35)

Исследования показывают, что значение у₀ для опор контакт­ной сети изменяется в очень небольших пределах, оставаясь всегда близким к . Это соответствует случаю, когда на опору дей­ствует только опрокидывающий момент, а горизонтальная и вер­тикальные силы равны нулю. Другими словами, второй член подкоренного выражения (4.35) всегда значительно меньше первого. Такое соотношение позволяет упростить выражение (4.35). Выне­сем h²/2 за знак радикала и используем известное положение тео­рии приближенных вычислений ( при a«1), тогда

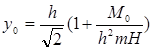                                                                                               (4.36)

Найдем значение у_о^з После возведения в степень множителя в скобках отбросим два члена уравнения из-за их малого значе­ния. Тогда

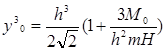                                                                                            (4.37)

Величину y₀³ из выражения (4.37) подставим в формулу (4.34) и после преобразований получим

                                                          (4.38)

 

Решим уравнение (4.38) относительно М₀:

 

                                                                                             (4.39)

 

Если на опору момент, то и фундамент действует только опрокидывающий момент, то

 и

Предположим, что в формуле (4.39)   Н = , тогда

 

                                                                                   (4.40)

 

В   выражениях  (4.39)   и (4.40)   не известно значение е. Оно может

быть найдено из условия, что е = (см. рис. 4.27). Так как а = N_p/ , то

                                       е=d/2-N_p /                                       (4.41)

где к = 0,7 — коэффициент однородности; _п — предельное давле­ние грунта на подошву фундамента (см. таблицу); b и d — ширина и толщина фундамента. Значение е примерно равно 0,4 d.

Определение допустимой нагрузки для фундамента. Приведен­ные выше выводы и расчетные формулы для определения предель­ной горизонтальной силы и предельного момента даны для неко­торых обезличенных условий. Согласно принятой терминологии условным назван фундамент призматической формы прямо­угольного поперечного сечения (без лежней или с лежнями), зако­панный на горизонтальной площадке при отсутствии в непосред­ственной близости железнодорожного пути и при нагрузке, в ко­торой доля постоянной составляет 35 %. Всякий фундамент, усло­вия работы которого будут отличаться от приведенных, называют заданным. Предельную нагрузку для заданного фундамента опре­деляют, умножая предельную нагрузку условного фундамента на коэффициенты условий работы, значения которых установлены опытным путем. В соответствии с этим предельную нагрузку для призматического фундамента другой формы и в других условиях работы определяют по выражению

                      М=М₀m_ф m_от m_вб m_у m_п m_нг                              (4.42)

где m — коэффициенты, учитывающие: m_ф — форму поперечного сечения; m_ОТ — очертание поверхности грунта в месте расположе­ния фундамента; m_вб — вибрации (колебания) грунта около фундамента от проходящих поездов; т_у — повышенное уплотне­ние грунта при забивке фундамента; m_нг — долю постоянной на­грузки в суммарной.

Коэффициент m_ф для фундамента без лежней прямоугольного сечения рекомендуется принимать равным единице, круглого — 0,9 и двутаврового —1,1 (при действии усилия вдоль его стенки, т.е.перпендикулярно полке). Коэффициент m_от при нагрузке, действу­ющей в плоскости, перпендикулярной бровке земляного полотна, определяют по рис. 4.28 в зависимости от очертания поверхности грунта в месте установки фундамента и направления горизонталь­ной нагрузки. Если нагрузка действует в плоскости, параллельной бровке земляного полотна, m_от принимают равным единице.

При вибрации (колебании) грунта около фундамента от прохо­дящих поездов, т.е. для опор, устанавливаемых в теле земляного полотна главных путей, коэффициент m_вб = 0,9, а при отсутствии колебаний m_вб = 1. Коэффициент т_y принимают равным единице для закапываемых фундаментов, т. е. устанавливаемых в котлова­не, вырытых вручную или буровой машиной; 1,2 — для свайных фундаментов сплошных сечений и пустотелых, забитых с закры­тым концом; 1,1 — для свайных пустотелых фундаментов, забитых с открытым концом, двутавровых и трехлучевых. Коэффициент m_п=1 при расположении фундамента за кюветом или при расстоя­нии от оси пути до ближайшей грани фундамента более 4 м, или при моменте, действующем в плоскости, параллельной оси пути m_п=1,2 — при моменте, действующем в сторону пути при расстоянии от оси ближайшего пути до передней грани фундамента менее 3,2 м (при расстоянии от 3,2 до 4 м m_п=1,1) и m_п=1,1 при моменте, действующем в сторону поля, и расстоянии от оси бли­жайшего пути до ближайшей грани фундамента до 4 м.

 

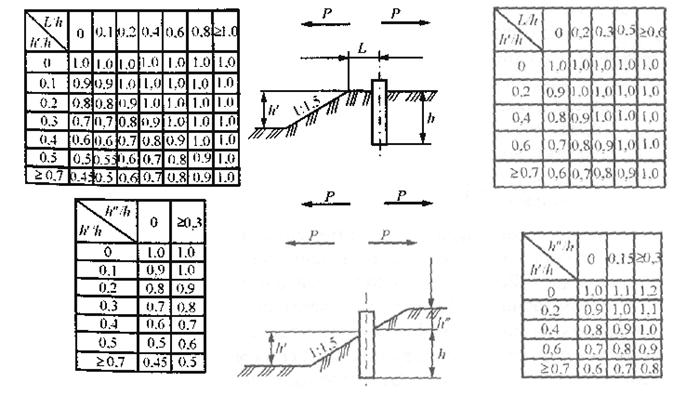
Рис. 4.28. Таблицы и схемы для определения коэффициента '»_от, учитывающего влияние очертания поверхности грунта

 

Перемещение фундамента связано со временем действия силы, поэтому временные нагрузки оказывают меньшее влияние, чем постоянные, поэтому коэффициент т_нг определяется по формуле

                                             m_нг = 1/(0,5+1,43),                                           (4.43)

где  — коэффициент, характеризующий долю постоянной нагруз­ки в суммарной.

Если  = 0,35, то m_нг = 1 (для условного фундамента все коэф­фициенты равны 1,0, а  = 0,35). При расчетных моментах М_рп (от постоянной нагрузки) и М_рп (от временной нагрузки), дейст­вующих в одном направлении,

                                    = М_рп/(М_рп+М_рв)                                                (4.44)

Выражение (4.44) верно при Н»h, т.е. практически всегда при расчете фундаментов опор контактной сети, так как высота опоры Н всегда > глубины заделки грунта h. Если действует только по­стоянная нагрузка ( = 1), то т_нг=0,5 (почти двойной коэффици­ент запаса). Если действует только временная нагрузка ( = 0), то м_нг=2, т.е. допускается вдвое большая нагрузка, чем предельная. При действии моментов М_рп и М_рв в противоположных направлениях, когда М_рп<М_рв,  м_нг= 2,0. Если М_рп > М_рв, то расчет выполняют только на действие момента М_рп при m_нг = 0,52.

Определим допустимое давление на подошву фундамента, учи-! тывая, что при расчетах фундамента всегда необходимо проверять его также на действие только вертикальной нагрузки. Вертикаль­ному перемещению фундамента препятствуют возникающие реак­ции грунта на подошву и сила трения между боковыми стенками фундамента и грунта. Это перемещение несколько увеличивается, если возникает вибрация грунта от проходящих поездов. В соот­ветствии с этим допустимая вертикальная нагрузка

                                                                                 (4.45)

где и — периметр попе­речного сечения фунда­мента (для фундамен­тов таврового, двутав­рового сечения пери­метр определяют по контурам, показанным на рис. 4.29); h — глуби­на фундамента;  — пре­дельное удельное сопро­тивление трения грунта по вертикальной поверхности фундамента (для закопанных фундаментов независимо от категории грунта ре­комендуется принимать 9,81 кПа); _п — предельное давление грунта на подошву фундамента (см. таблицу); F_п — площадь подошвы за­капываемого фундамента или плиты, на которую он опирается.

Свайные фундаменты, как правило, на вертикальную нагрузку не проверяют.

Для закрепления поддерживающих и опорных конструкций в грунте разработаны типовые способы и конструкции подземной части, включая и непосредственную заделку железобетонных опор. При выборе стремятся использовать типовые решения. Способ зак­репления опор в грунте выбирают по нормативному изгибающему моменту опоры. При этом учитывают все условия, определяемые местом установки опоры: габарит относительно оси пути, направ­ление действия опрокидывающего момента, характеристики грун­та, поперечный профиль (площадка, насыпь или выемка).

 

 

Рис. 4.29. Расчетная схема для определения расчетного периметра таврового (а), двутав­рового (б) и трехлучевого (в) сечений