2.1. Гидростатика
Основные понятия. Гидравликой называется прикладная наука, изучающая законы равновесия и движения жидкостей и способы их практического использования.
Жидкостью в физике считается тело, обладающее текучестью. Вследствие слабых связей между собой частицы жидкости обладают высокой степенью подвижности. Поэтому жидкое тело в отличие от твердого не имеет собственной формы и принимает форму сосуда, в котором оно находится.
Гидравлика состоит из двух основных разделов: гидростатики и гидродинамики. В гидростатике рассматриваются законы равновесия жидкостей, в гидродинамике — законы их движения.
С точки зрения гидравлики под термином «жидкость» понимают не только жидкие, но и газообразные тела. В связи с этим жидкости делят на капельные и газообразные.
В гидравлике преимущественно рассматриваются капельно-жидкие тела, характеризующиеся очень малой сжимаемостью. Однако при давлениях, близких к атмосферному, и газы, которые характерны большой сжимаемостью при повышении давления, ведут себя как практически несжимаемые жидкости и подчиняются основным законам гидравлики.
Особенности движения газов при иных давлениях и температурах, когда заметно проявляются их отличия от капельных жидкостей, изучаются в аэродинамике и газовой динамике.
Физические свойства жидкостей. В гидравлике используются основные свойства жидкостей, изучаемые в курсах физики, а именно удельный
вес, плотность, сжимаемость, тепловое расширение и вязкость, которые кратко рассмотрены ниже. Как и все физические величины, характеристики этих свойств могут измеряться в различных системах единиц измерения, из которых наиболее распространена Международная система (СИ) как более универсальная.
Удельным (или объемным) весом у жидкости называют вес жидкости в единице объема, т. е. отношение
7=0/1/, (2.1)
где й — вес (сила тяжести) определенного количества (определенной массы) жидкости; V — объем этого количества жидкости.
Размерность удельного веса в соответствии с формулой (2.1) равна отношению единицы силы к единице объема, т. е. Н/м3.
Плотность р жидкости представляет величину ее массы в единице объема:
Р = М/К, (2.2) где М — масса жидкости в объеме V.
Размерность плотности — кг/м3. Так как вес (сила тяжести) и масса тела связаны между собой на основании второго закона Ньютона ((5 = = Mg, где £ = 9,81 м/с2 — ускорение свободного падения), то аналогично связаны между собой удельный вес и плотность:
У = 98- (2-3)
Отсюда p = y/g. Поэтому размерность плотности представляет отношение размерностей удельного веса и ускорения.
Удельный объем и — объем единицы массы—величина, обратная плотности:
и = У/М=\/р. (2.4)
Его единица — м3/кг.
Удельный вес, плотность и удельный объем капельных жидкостей и газов не являются постоянными величинами, они зависят от давления и температуры. При повышении температуры жидкости ее удельный вес и плотность уменьшаются, а удельный объем увеличивается. Тепловое расширение жидкостей характеризуется температурным коэффициентом объемного расширения р<, который равен отношению приращения объема АУ к первоначальному объему Уо и приращению температуры Л/ (при постоянном давлении):
(2.5)
Размерность р( обратна размерности температуры.
Из формулы (2.5) можно определить приращение объема жидкости при нагревании:
ДК=р,1/0Л<. (2.6)
Для капельных жидкостей величина Р/ относительно невелика (для воды 0,0004 при температуре 20—100 °С) и приращение их объема при нагревании незначительно. Но все же нагревание воды в системе дизеля, объем которой составляет более 1200 л, от 20 до 90 °С изменяет эту величину на 40 л. Газы вообще характерны высокими значениями
При повышении давления удельный вес и плотность жидкости увеличиваются, а удельный объем уменьшается. Сжимаемость жидкостей характеризуется коэффициентом объемного сжатия рр, который равен относительному уменьшению объема жидкости на единицу приращения давления Др при неизменяемой температуре:
![]()
где АУ—изменение объема (минус в формуле указывает на его уменьшение).
Размерность рр обратна размерности давления.
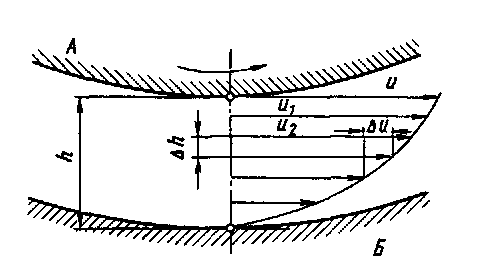
Рис. 2.1. Внутреннее трение в слое жидкости
Уменьшение объема жидкости при сжатии
(2.8)
Величина рр для капельных жидкостей также очень мала (РР = = 0,0005, если давление измеряется в МПа), поэтому сжимаемостью капельных жидкостей обычно можно пренебрегать (их считают в гидравлике несжимаемыми). Необходимо отметить также, что жидкости практически не сопротивляются растяжению.
Вязкость — свойство жидкости оказывать сопротивление относительному перемещению ее частиц.
Предположим, жидкость (масло) заполняет тонкий зазор между вращающимся валом А и неподвижным подшипником Б (рис. 2.1). Опыт показывает, что частицы жидкости, непосредственно соприкасающиеся с граничными стенками, как бы прилипают к ним и имеют одинаковую с ним скорость. Следовательно, слой жидкости, примыкающий к валу А, будет перемещаться со скоростью вала «, а слой, соприкасающийся с подшипником, будет неподвижен. Таким образом, скорость промежуточных слоев жидкости в зазоре будет различной и каждый из них будет перемещаться (сдвигаться) относительно соседних слоев. Внутреннее трение в жидкости оказывает сопротивление такому сдвигу с силой по площади сдвига 5.
Удельная сила трения т («тау») — напряжение сдвига:
где ц («мю») — динамическая вязкость; Лы/АЛ — градиент скорости в слое жидкости: отношение разности скоростей
смежных слоев ЖИДКОСТИ (Ли = Ы) — Иг)
к расстоянию ДЛ между ними (см. рис. 2.1).
Единица измерения ц — Н-с/м2, или Па-с. Эта единица очень значительна по своему размеру. Поэтому применяют дольную единицу— миллипаскаль-секунду (мПа>с).
В гидравлике используется также понятие кинематической вязкости V («ню»):![]()
где р — плотность жидкости.
Единица измерения V — м2/с. Вязкость характеризует степень подвижности частиц жидкости. Вода имеет низкую вязкость, нефтепродукты (различные масла, дизельное топливо) отличаются более высокой вязкостью.
Вязкость жидкостей уменьшается при повышении их температуры.
Вязкие свойства и сжимаемость жидкостей значительно усложняют рассмотрение многих вопросов их движения. Поэтому в гидравлике часто пользуются понятием идеальной жидкости, т. е. условной жидкости, не обладающей вязкостью и абсолютно несжимаемой. Такая жидкость имеет постоянную плотность, не обладает внутренним трением и, следовательно, не оказывает сопротивления перемещению. Идеальных жидкостей в природе не бывает, но использование этого понятия облегчает выяснение основных законо-
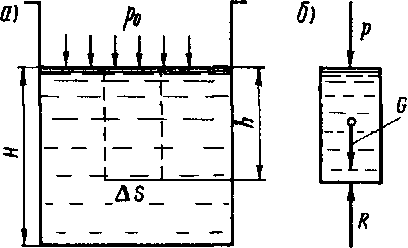
Рис. 2.2. К выводу основного уравнения гидростатики:
а — сосуд с жидкостью; 6 — элемент объема жидкости
мерностей гидравлики, используя которые применительно к реальным жидкостям, необходимо учитывать поправки на их вязкость и сжимаемость.
Основное уравнение гидростатики.
В открытом сосуде с жидкостью, находящейся в покое (рис. 2.2, а), представим мысленно на глубине А площадку Л5 и рассмотрим условия ее равновесия. Для этого выделим элемент объема жидкости, расположенный над площадкой (рис. 2.2, б), заменив его связи с окружающим пространством внешними силами.
В горизонтальном направлении на боковую поверхность цилиндра действуют силы давления окружающей его жидкости. Они уравновешиваются как равные и противоположно направленные.
В вертикальном направлении на элемент действуют: сила внешнего давления Р = р0\3, где р0 — внешнее давление на свободную поверхность жидкости (для открытого сосуда— атмосферное давление ра — Ро)\ сила тяжести б массы жидкости в объеме элемента (й =yhAS = pghAS).
Обе эти силы действуют вниз. Однако элемент, как и вся жидкость в сосуде, находится в равновесии. Такое равновесие возможно лишь при наличии уравновешивающей силы /?, действующей на площадку со стороны остального объема жидкости, т. е. снизу вверх. Эту распределенную по площадке силу можно представить, так же как и силу внешнего давления, в виде произведения давления на площадь: # = рЛ5. Величина р = Р/АБ носит название гидростатического давления.
Гидростатическое давление характерно двумя важными свойствами: оно всегда направлено перпендикулярно к площадке, на которую действует; величина гидростатического давления в любой точке объема жидкости не зависит от положения (угла наклона) площадки, на которую оно действует (иными словами, в данной точке оно одинаково по всем направлениям).
Условием равновесия выделенного объема в вертикальном направлении будет уравнение /? — Р—(7 = 0 или
![]()
Отсюда
![]()
Уравнение (2.11) называют основным уравнением гидростатики. Оно показывает, что гидростатическое давление в любой точке внутри жидкости равно давлению на ее свободную поверхность, сложенному с давлением столба жидкости, высота которого равна глубине точки, в которой измеряется давление.
Гидростатическое давление по формуле (2.11) называют полным, или абсолютным.
Избыточное (или манометрическое) давление
Риэв=р —Ро = р#А = уА. (2-12)
Измерение давления. Как видно из уравнения (2.12), избыточное давление совпадает с давлением столба жидкости. Это совпадение указывает на простой и удобный способ измерения небольших избыточных давлений — по высоте столба жидкости.
Простейшим прибором такого типа является пьезометр (рис. 2.3, а) — вертикальная прозрачная трубка, присоединенная к сосуду с жидкостью своим нижним концом. Верхний конец трубки открыт. Если в сосуде давление атмосферное—уровни жидкости в нем и в трубке будут одинаковы. Если же в сосуде давление выше атмосферного, столб жидкости в трубке будет выше уровня в сосуде на высоту Л, которая называется пьезометрической высотой и является по уравнению (2.12) мерой избыточного давления. Этот же способ используется в общеизвестном и-образном манометре (рис. 2.3, б), применяемом обычно для измерений малых давлений в воздушных и газовых потоках. Если высота трубки в таких приборах не превышает 1 м, то наибольшее избыточное давление, которое можно изме-
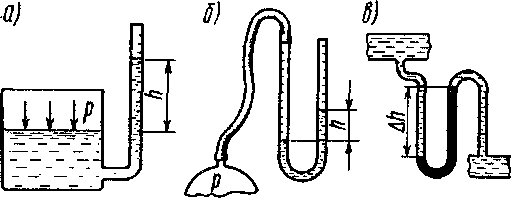
Рис. 2.3. Измерение гидростатического давления:
а — пьезометр; б — и-образный манометр; в — дифференциальный манометр
рить, не превышает 10 кПа. Для измерений больших давлений применяют манометры с ртутью, удельный вес которой в 13,6 раза больше удельного веса воды. Это позволяет или увеличить диапазон измеряемых давлений, или уменьшить высоту трубок. Для измерения разности давлений ДА в разных сосудах или в различных участках трубопровода применяют дифференциальные манометры (рис. 2.3, в).
Для измерения высоких давлений применяют металлические манометры (пружинные и мембранные).
Закон Паскаля. Из основного уравнения гидростатики (2.11) следует, что внешнее давление, приложенное к свободной поверхности жидкости, находящейся в ограниченном сосуде, передается в любую точку жидкости без изменения. Иными словами: давление, приложенное в каком-то участке замкнутой гидравлической системы, сообщается всей жидкости, находящейся в системе.
Это положение, называемое законом Паскаля, широко используется в технике в различных гидравлических устройствах, предназначенных для «выигрыша» в силе (грузоподъемные устройства, домкраты, прессы) или передачи силы на расстояние (гидропривод). Устройства, основанные на законе Паскаля, широко применяются и в тепловозостроении. Это, например, гидравлическое управление иглой форсунки дизеля, гидростатический привод вентиляторов, сервомотор регулято-
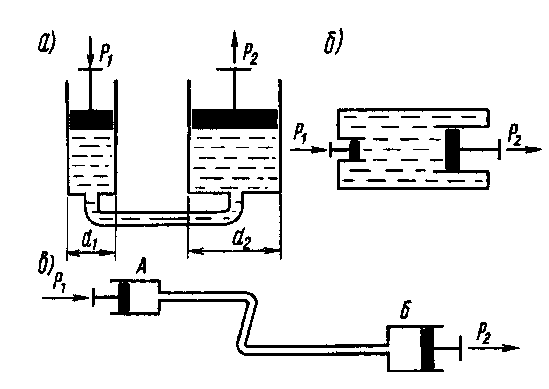
Рис. 2.4. Схемы гидростатического привода
ра частоты вращения вала дизеля и т. п.
Принципы их действия иллюстрируются схемами рис. 2.4. Если соединить два цилиндра диаметрами (1\ и сЬ, заполненные жидкостью (рис. 2.4, а), или просто расположить два разных поршня в одном резервуаре (рис. 2.4, б), то, приложив силу Р\ к поршню малого цилиндра, мы создадим во всей системе давление р = 4Р|/(л.<з?). Под действием этого давления поршень большого цилиндра при перемещении способен преодолеть гораздо большее усилие:
значение которого зависит от квадрата соотношения диаметров этих цилиндров. Так, например, устроены гидравлические домкраты. На основе этого принципа создаются гидравлические прессы, способные развивать колоссальные усилия (тысячи и десятки тысяч тонн).
Схема (рис. 2.4, в) показывает передачу управляющего усилия на
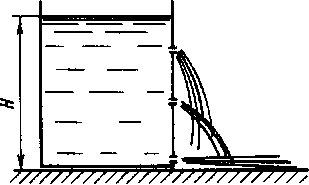
Рис. 2.5. К определению давления жидкости на вертикальную стейку
расстояние: приложив силу Р\ к поршню цилиндра Л, соединенного трубопроводом с цилиндром Б, мы заставим перемещаться его поршень, несмотря на то, что цилиндры могут быть удалены друг от друга.
Давление жидкости на стенку сосуда в соответствии с основным законом гидростатики неодинаково по высоте.
Это наглядно видно на примере вертикального резервуара (рис. 2.5). Если просверлить в его боковой стенке несколько отверстий на разной высоте, то мы увидим, что вода будет вытекать из них в горизонтальном направлении и дальность струи будет тем больше, чем ниже отверстие. Этот опыт подтверждает также, что вода оказывает именно боковое давление на стенку, перпендикулярное к ее поверхности. Если требуется определить силу давления жидкости на плоскую стенку сосуда, то необходимо иметь в виду, что на уровне свободной поверхности давление на стенку равно внешнему давлению ро(Л = 0), а на дно сосуда давление р = Ро + рёН. Так как гидростатическое давление по уравнению (2.11) линейно зависит от глубины, то, чтобы вычислить силу давления на всю стенку, достаточно определить среднее давление: рср = ро + р£#/2 и умножить его на площадь стенки.










